지난번에는 매칭에 대해서 글을 썼는데, 오늘은 성향점수(Propensity Score : 이하 PS) 매칭, 역확률 가중치(Inverse Probability Weighting : 이하 ipw)에 대해 글을 써보려고 합니다.
- 성향점수란 무엇인가
- 역확률 가중치란 무엇인가
- 성향점수를 활용하는 매칭과 역확률가중치는 어떻게 다른가
의 이야기를 다루려고 합니다.
1. 매칭
이전 글에 다루기는 했지만 다시 간략하게 요약해보겠습니다.
매칭은 처치 집단과 통제 집단 간 공변량(Covariate)이 다를 때, 비슷한 특성을 가진 데이터끼리 짝지어 매칭시키고, 매칭된 데이터끼리 결과변수를 비교하는 개념입니다.
X_1과 X_2 변수를 기준으로 각 셀마다 매칭된 데이터를 확인할 수 있고, 대조군과 처치군의 결과변수 평균 차이를 구해 처치 효과를 추정할 수 있습니다.
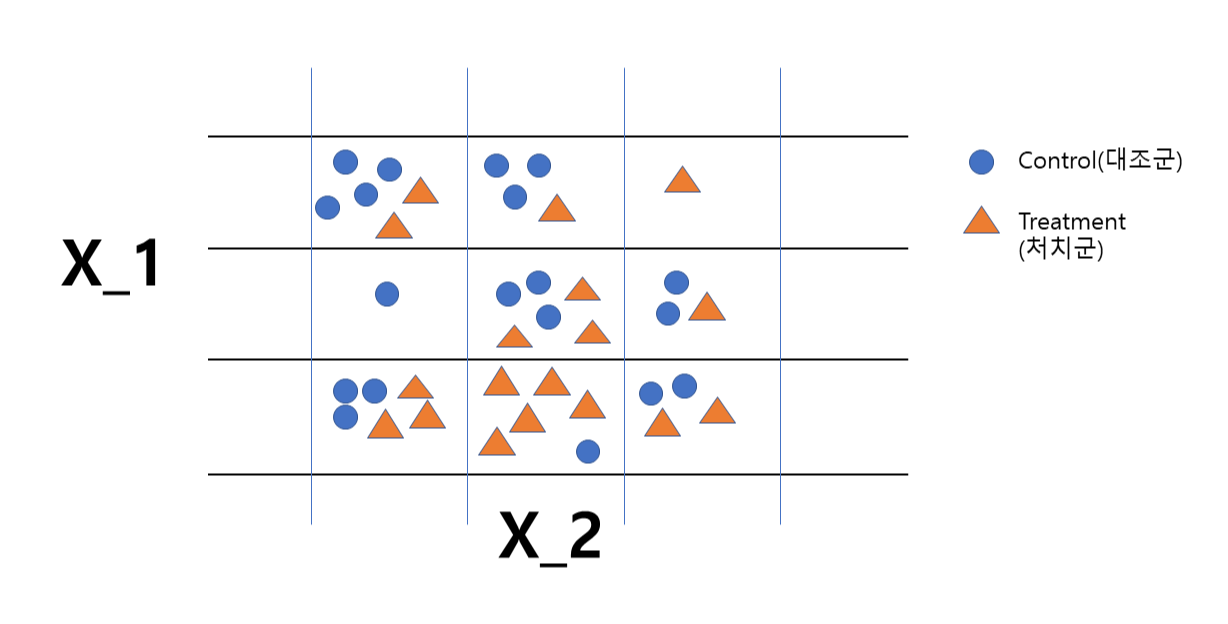
이 때, 처치군이나 대조군이 하나씩만 들어있는 셀은 가중치를 낮게 주거나 아예 주지 않고,
처치군(Treatment) 기준으로 설명변수(X_1, X_2)가 많이 분포된 쪽은 가중치를 많이 주고, 적게 분포된 쪽은 가중치를 적게 줘서 결과변수의 최종적인 가중치를 구합니다.
조금 더 현실적인 예를 들어보자면.. (사실 깊게 생각한 예시는 아니라 적절하지 않을 수 있습니다..)
https://www.hani.co.kr/arti/society/schooling/1071099.html
올해도 이과가 휩쓸었다…겉만 통합형 수능이 부른 ‘문과 몰락’
수학 1등급 93%가 ‘미적분·기하’ 선택
www.hani.co.kr
https://www.chosun.com/national/education/2023/02/18/ULL3FCZU6VFVNKQR72GN5SDJT4/
[NOW] 초등 4학년 ‘의대 입시반’까지 생겼다
NOW 초등 4학년 의대 입시반까지 생겼다 의사가 최고 인식에 부모는 선행학습 욕심, 학원은 불안 마케팅
www.chosun.com
문, 이과 선택 여부에 따라 국어, 영어, 수학 성적 분포는 다를 것입니다.
그런데 현재 수능 시험은 수학의 변별력이 큰 상태로 운영이 되고 있다고 합니다.
수학을 잘하는 학생이 이과에 있을 확률이 높기 때문에 현재는 기사처럼 '이과가 휩쓸었다'는 이야기가 나오고 있지만, 이 단면만 보고 '이과가 더 똑똑하다'라고 단언하기는 어렵습니다.
왜나햐면 국어와 영어가 변별력이 높게 출제된다면, 이 때는 판도가 달라질 수도 있기 때문입니다.
만일 고1의 국어, 영어, 수학 성적이 비슷한 학생들끼리 매칭시켜서 문과/이과(처치변수) 여부에 따라 진짜 뭔가를 휩쓸었는지 아닌지를 비교하는 것을 매칭이라고 볼 수 있을 것입니다.
2. 성향점수
그러나 매칭에 필요한 공변량이 많아질수록 차원은 점점 높아지게 되고, 셀 안에 매칭되는 데이터가 적어질 우려가 있습니다. 차원의 저주(Curse of Dimensionality)가 발생하게 된다고도 볼 수 있는 것이지요.
그래서 공변량의 특징을 단일 값 하나로 압축한 상태로 매칭시키는 개념이 등장하게 됩니다.
압축된 하나의 단일 값을 성향점수(PS)라고 하고, 보통 logit이나 probit 모형을 사용해서 구합니다.
그리고 위의 성향점수를 기반으로 매칭하는 것을 성향점수 매칭(Propensity Score matching : 이하 PSM)이라고 합니다.
그리고 대략 아래 단계를 따라 분석을 진행합니다.
- 처치 여부에 따라 성향점수를 구한다.
- 처치 여부별로 성향점수 분포를 확인한다. 그리고 공통지지(Common Support)가 있는지 본다.
- 필요하다면, 양 극단의 성향점수에 분포한 데이터를 버린다.
- 성향점수를 기준으로 데이터를 매칭한다.
- 이후 나름대로 가중치를 줘서 매칭한 데이터끼리 가중평균을 구한다.
위 단계를 거치기 전에, 다차원의 정보를 하나의 값으로 압축한 값으로 매칭을 해도 문제가 없을지에 대한 의문이 있을 수 있을 것 같습니다.

이미 훌륭한 증명들이 많이 있어 증명을 하지는 않겠지만(만약 증명이 궁금하시다면, 위 이미지 출처를 참고하시면 될 것 같아요!) 공변량이 주어졌을 때, CIA가 성립한다면 공변량을 하나로 압축한 성향점수로도 CIA가 성립됩니다.
다만, 공통지지(Common Support)가 있는지를 보는 건 매우 중요한데, 처치 여부별로 성향점수가 공통되는 부분이 거의 없다면 사실상 매칭이 불가능하기 때문입니다.
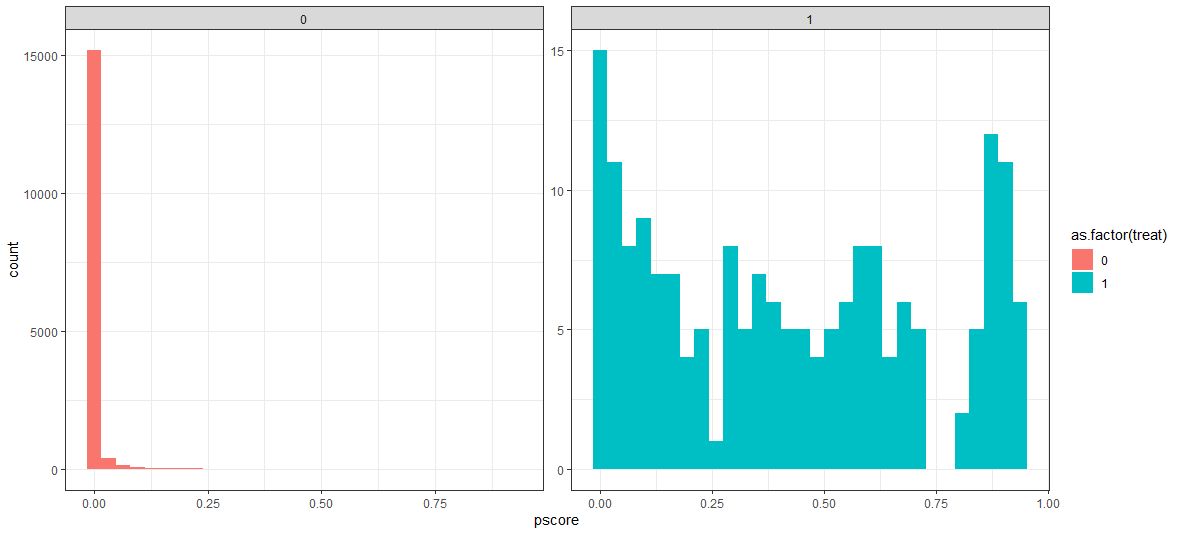
만일 처치 여부별로 성향점수 분포가 크게 차이가 나서 겹치는 부분이 없다면, 사실상 매칭이 불가능합니다.
이 때, 양극단치 성향점수를 버리고 다시 비교해볼 수 있을텐데,
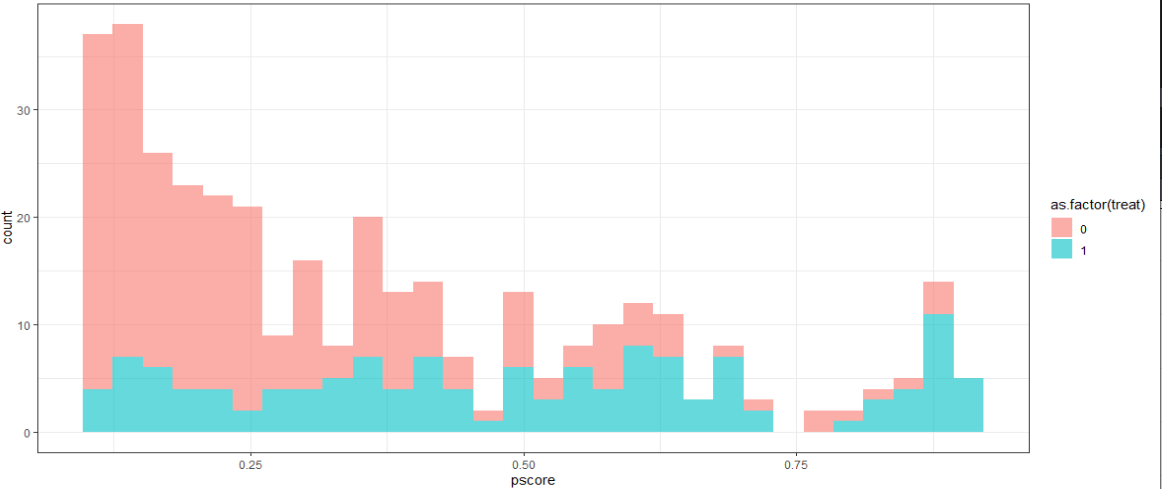
데이터를 꽤나 많이 버려오기는 했지만 그래도 처치군과 대조군 간에 겹치는 성향점수가 꽤 있어서 매칭을 진행할 수 있게 됩니다.
3. 역확률 가중치
위에서는 성향점수를 활용한 매칭에 대해 말씀드렸지만, 성향점수를 활용해서 인과추론을 할 수 있는 방법 중에 역확률 가중치(ipw)도 있습니다.
매칭이 성질이 비슷한 데이터끼리만 남기고, 매칭이 어려운 데이터는 버려가면서 처치군과 대조군을 비교하는 방법이라고 하면,
역확률 가중치는 성향점수의 역을 가중치로 줘서, 만일 주어진 분포에서 처치될 가능성이 낮더라도 처치가 안 된 데이터와 1대 1로 비교할 수 있도록 데이터를 불려 와서 비교하는 방법이라고 볼 수 있습니다.
너무 많이 생략이 된 예시이기는 하지만, 만일 특정 조건에서 대조군에 비해 현저히 처치군이 적다고 할 때,
- 매칭은 처치군과 성질이 비슷한 데이터만 남겨놓고, 잔디 깎듯 밀어버리는 느낌이라면,
- 역확률 가중치는 처치군의 데이터가 부족한 만큼, 성향점수에 반비례하는 정도로 데이터를 복제
(그림자 분신)시켜서 대조군과 비교하도록 만들어줍니다.


4. 매칭과 역확률 가중치의 비교
두 방법 모두 성향점수를 활용한다는 점은 공통적입니다. 즉, 성향점수를 잘못 계산하면 뒷단의 인과분석이 모두 잘못되어 버릴 가능성이 높다는 뜻이지요.
하지만 어떤 때 매칭을 써야하는 것인지, 어떤 때 역확률 가중치를 써야하는지는 다소 모호한 부분이 있습니다.
공부를 하긴 했어도, 제가 마음으로 이해하지는 못해서 이 부분은 2022년 진행됐던 Korea Summer Workshop on Causal Inference 자료를 참고로 가져왔습니다.
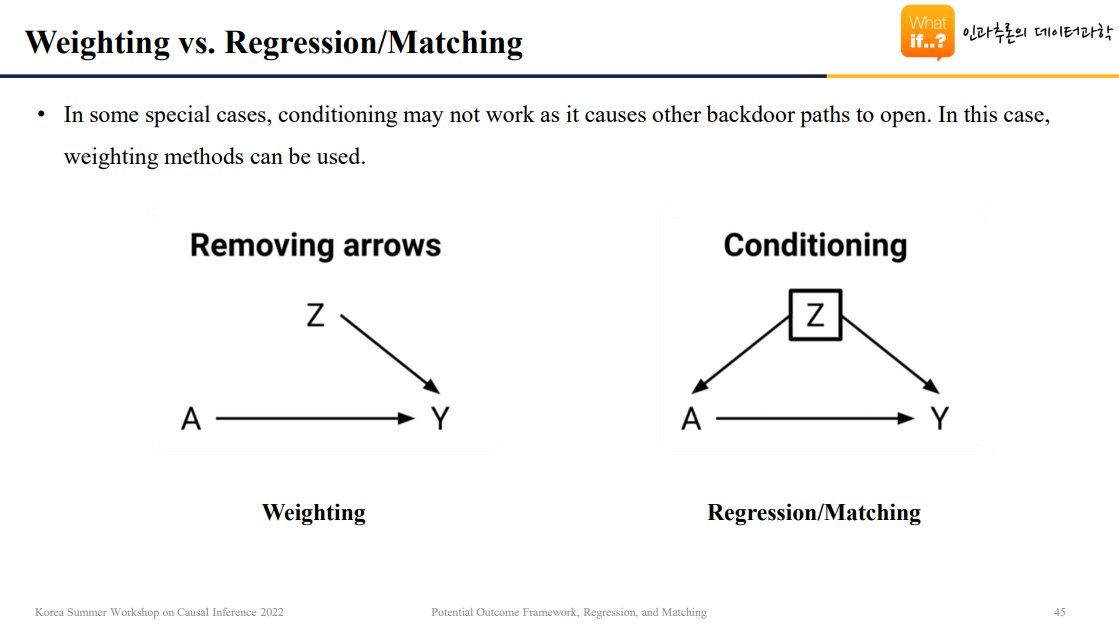
위 자료에서는 매칭을 하거나, Regression을 쓰거나 결국 이 두 방법은 Conditioning한 방법이라고 합니다.
Conditioning은 특정 변수가 주어진 상태(위 예시에서는 Z)에서 처치 여부(위 예시에서는 A)가 어느 정도 효과를 갖는지를 파악하는 것입니다.
Removing arrow라고 되어 있는 부분은 DAG 관점에서 설명하는 부분이기는 하지만, 간략히 설명하면 Z가 A에 미치는 영향력을 없애버리는 방식으로 A가 Y에 얼마나 영향을 미치는지를 파악하는 방법입니다. (자세하게 알려면 do-Calculus에 대해서 알아야 해요..)
강제로 영향력을 없앤다는 것을 직관적으로 설명하면 만약 나이의 영향력이 분석에 중요하다고 가정할 때,
Conditioning은 `나이를 바꿀 수는 없으니 이를 고정시켜 놓은 상태에서 분석하자!`의 느낌이라면
Removing Arrow는 `나이를 일괄 20대로 바꿔놓고 분석하자!`의 느낌이라고 보시면 될 것 같아요.
역확률 가중치는 실제 분포에 따른 처치 확률을 고려하지 않고, 성향점수의 역확률로 가중치를 줘서 일괄적으로 데이터를 다 바꿔놓았기 때문에 Removing Arrow를 사용했다고 볼 수 있습니다.
Removing Arrow는
- Conditioning을 사용하지 못하는 경우에 사용 가능
- Random Assignment에 가깝게 분석을 진행할 수 있다는 점에서 이점이 있다고 합니다.
이하 글 작성에 참고한 자료 링크로 마무리하겠습니다.
1. mixtape - Matching and Subclassification
매칭과 성향점수 분석에 대해 좀 더 자세히 알 수 있어요.
2. 인과추론의 데이터 과학 - Bootcamp 2-4. 매칭과 역확률 가중치
역확률 가중치에 대해 좀 더 자세히 알고 싶을 때 보면 좋습니다!
3. https://pizzathief.oopy.io/causal-intervention
인과 추론 3. 개입
이 글은 Causal Inference in Statistics: A Primer의 4장 내용을 기반으로 작성하였습니다. 읽기 전에 인과 추론에서의 그래프 모델 소개를 읽고 오시면 쉽습니다.
pizzathief.oopy.io
Do-calculs에 대해 직관적으로 이해할 수 있도록 쉽게 글을 써주셔서 인과추론 공부에 도움이 되었습니다.
'Statistics' 카테고리의 다른 글
| 인과추론 학습기 - 05. 2SLS와 LATE의 기본 개념 (2) | 2023.06.29 |
|---|---|
| 인과추론 학습기 - 04. 도구변수의 기본 개념 (2) | 2023.05.20 |
| 인과추론 학습기 - 02. 매칭 추정량과 회귀분석 (matching, regression) (1) | 2023.03.11 |
| 인과추론 학습기 - 01. 인과추론의 핵심문제 (선택편의와 교락) (0) | 2023.02.19 |
| 인과추론 학습기 - 00. 왜 인과추론인가? (공부이유, 학습자료) (0) | 2023.01.08 |
지난번에는 매칭에 대해서 글을 썼는데, 오늘은 성향점수(Propensity Score : 이하 PS) 매칭, 역확률 가중치(Inverse Probability Weighting : 이하 ipw)에 대해 글을 써보려고 합니다.
- 성향점수란 무엇인가
- 역확률 가중치란 무엇인가
- 성향점수를 활용하는 매칭과 역확률가중치는 어떻게 다른가
의 이야기를 다루려고 합니다.
1. 매칭
이전 글에 다루기는 했지만 다시 간략하게 요약해보겠습니다.
매칭은 처치 집단과 통제 집단 간 공변량(Covariate)이 다를 때, 비슷한 특성을 가진 데이터끼리 짝지어 매칭시키고, 매칭된 데이터끼리 결과변수를 비교하는 개념입니다.
X_1과 X_2 변수를 기준으로 각 셀마다 매칭된 데이터를 확인할 수 있고, 대조군과 처치군의 결과변수 평균 차이를 구해 처치 효과를 추정할 수 있습니다.

이 때, 처치군이나 대조군이 하나씩만 들어있는 셀은 가중치를 낮게 주거나 아예 주지 않고,
처치군(Treatment) 기준으로 설명변수(X_1, X_2)가 많이 분포된 쪽은 가중치를 많이 주고, 적게 분포된 쪽은 가중치를 적게 줘서 결과변수의 최종적인 가중치를 구합니다.
조금 더 현실적인 예를 들어보자면.. (사실 깊게 생각한 예시는 아니라 적절하지 않을 수 있습니다..)
https://www.hani.co.kr/arti/society/schooling/1071099.html
올해도 이과가 휩쓸었다…겉만 통합형 수능이 부른 ‘문과 몰락’
수학 1등급 93%가 ‘미적분·기하’ 선택
www.hani.co.kr
https://www.chosun.com/national/education/2023/02/18/ULL3FCZU6VFVNKQR72GN5SDJT4/
[NOW] 초등 4학년 ‘의대 입시반’까지 생겼다
NOW 초등 4학년 의대 입시반까지 생겼다 의사가 최고 인식에 부모는 선행학습 욕심, 학원은 불안 마케팅
www.chosun.com
문, 이과 선택 여부에 따라 국어, 영어, 수학 성적 분포는 다를 것입니다.
그런데 현재 수능 시험은 수학의 변별력이 큰 상태로 운영이 되고 있다고 합니다.
수학을 잘하는 학생이 이과에 있을 확률이 높기 때문에 현재는 기사처럼 '이과가 휩쓸었다'는 이야기가 나오고 있지만, 이 단면만 보고 '이과가 더 똑똑하다'라고 단언하기는 어렵습니다.
왜나햐면 국어와 영어가 변별력이 높게 출제된다면, 이 때는 판도가 달라질 수도 있기 때문입니다.
만일 고1의 국어, 영어, 수학 성적이 비슷한 학생들끼리 매칭시켜서 문과/이과(처치변수) 여부에 따라 진짜 뭔가를 휩쓸었는지 아닌지를 비교하는 것을 매칭이라고 볼 수 있을 것입니다.
2. 성향점수
그러나 매칭에 필요한 공변량이 많아질수록 차원은 점점 높아지게 되고, 셀 안에 매칭되는 데이터가 적어질 우려가 있습니다. 차원의 저주(Curse of Dimensionality)가 발생하게 된다고도 볼 수 있는 것이지요.
그래서 공변량의 특징을 단일 값 하나로 압축한 상태로 매칭시키는 개념이 등장하게 됩니다.
압축된 하나의 단일 값을 성향점수(PS)라고 하고, 보통 logit이나 probit 모형을 사용해서 구합니다.
그리고 위의 성향점수를 기반으로 매칭하는 것을 성향점수 매칭(Propensity Score matching : 이하 PSM)이라고 합니다.
그리고 대략 아래 단계를 따라 분석을 진행합니다.
- 처치 여부에 따라 성향점수를 구한다.
- 처치 여부별로 성향점수 분포를 확인한다. 그리고 공통지지(Common Support)가 있는지 본다.
- 필요하다면, 양 극단의 성향점수에 분포한 데이터를 버린다.
- 성향점수를 기준으로 데이터를 매칭한다.
- 이후 나름대로 가중치를 줘서 매칭한 데이터끼리 가중평균을 구한다.
위 단계를 거치기 전에, 다차원의 정보를 하나의 값으로 압축한 값으로 매칭을 해도 문제가 없을지에 대한 의문이 있을 수 있을 것 같습니다.

이미 훌륭한 증명들이 많이 있어 증명을 하지는 않겠지만(만약 증명이 궁금하시다면, 위 이미지 출처를 참고하시면 될 것 같아요!) 공변량이 주어졌을 때, CIA가 성립한다면 공변량을 하나로 압축한 성향점수로도 CIA가 성립됩니다.
다만, 공통지지(Common Support)가 있는지를 보는 건 매우 중요한데, 처치 여부별로 성향점수가 공통되는 부분이 거의 없다면 사실상 매칭이 불가능하기 때문입니다.

만일 처치 여부별로 성향점수 분포가 크게 차이가 나서 겹치는 부분이 없다면, 사실상 매칭이 불가능합니다.
이 때, 양극단치 성향점수를 버리고 다시 비교해볼 수 있을텐데,

데이터를 꽤나 많이 버려오기는 했지만 그래도 처치군과 대조군 간에 겹치는 성향점수가 꽤 있어서 매칭을 진행할 수 있게 됩니다.
3. 역확률 가중치
위에서는 성향점수를 활용한 매칭에 대해 말씀드렸지만, 성향점수를 활용해서 인과추론을 할 수 있는 방법 중에 역확률 가중치(ipw)도 있습니다.
매칭이 성질이 비슷한 데이터끼리만 남기고, 매칭이 어려운 데이터는 버려가면서 처치군과 대조군을 비교하는 방법이라고 하면,
역확률 가중치는 성향점수의 역을 가중치로 줘서, 만일 주어진 분포에서 처치될 가능성이 낮더라도 처치가 안 된 데이터와 1대 1로 비교할 수 있도록 데이터를 불려 와서 비교하는 방법이라고 볼 수 있습니다.
너무 많이 생략이 된 예시이기는 하지만, 만일 특정 조건에서 대조군에 비해 현저히 처치군이 적다고 할 때,
- 매칭은 처치군과 성질이 비슷한 데이터만 남겨놓고, 잔디 깎듯 밀어버리는 느낌이라면,
- 역확률 가중치는 처치군의 데이터가 부족한 만큼, 성향점수에 반비례하는 정도로 데이터를 복제
(그림자 분신)시켜서 대조군과 비교하도록 만들어줍니다.


4. 매칭과 역확률 가중치의 비교
두 방법 모두 성향점수를 활용한다는 점은 공통적입니다. 즉, 성향점수를 잘못 계산하면 뒷단의 인과분석이 모두 잘못되어 버릴 가능성이 높다는 뜻이지요.
하지만 어떤 때 매칭을 써야하는 것인지, 어떤 때 역확률 가중치를 써야하는지는 다소 모호한 부분이 있습니다.
공부를 하긴 했어도, 제가 마음으로 이해하지는 못해서 이 부분은 2022년 진행됐던 Korea Summer Workshop on Causal Inference 자료를 참고로 가져왔습니다.

위 자료에서는 매칭을 하거나, Regression을 쓰거나 결국 이 두 방법은 Conditioning한 방법이라고 합니다.
Conditioning은 특정 변수가 주어진 상태(위 예시에서는 Z)에서 처치 여부(위 예시에서는 A)가 어느 정도 효과를 갖는지를 파악하는 것입니다.
Removing arrow라고 되어 있는 부분은 DAG 관점에서 설명하는 부분이기는 하지만, 간략히 설명하면 Z가 A에 미치는 영향력을 없애버리는 방식으로 A가 Y에 얼마나 영향을 미치는지를 파악하는 방법입니다. (자세하게 알려면 do-Calculus에 대해서 알아야 해요..)
강제로 영향력을 없앤다는 것을 직관적으로 설명하면 만약 나이의 영향력이 분석에 중요하다고 가정할 때,
Conditioning은 `나이를 바꿀 수는 없으니 이를 고정시켜 놓은 상태에서 분석하자!`의 느낌이라면
Removing Arrow는 `나이를 일괄 20대로 바꿔놓고 분석하자!`의 느낌이라고 보시면 될 것 같아요.
역확률 가중치는 실제 분포에 따른 처치 확률을 고려하지 않고, 성향점수의 역확률로 가중치를 줘서 일괄적으로 데이터를 다 바꿔놓았기 때문에 Removing Arrow를 사용했다고 볼 수 있습니다.
Removing Arrow는
- Conditioning을 사용하지 못하는 경우에 사용 가능
- Random Assignment에 가깝게 분석을 진행할 수 있다는 점에서 이점이 있다고 합니다.
이하 글 작성에 참고한 자료 링크로 마무리하겠습니다.
1. mixtape - Matching and Subclassification
매칭과 성향점수 분석에 대해 좀 더 자세히 알 수 있어요.
2. 인과추론의 데이터 과학 - Bootcamp 2-4. 매칭과 역확률 가중치
역확률 가중치에 대해 좀 더 자세히 알고 싶을 때 보면 좋습니다!
3. https://pizzathief.oopy.io/causal-intervention
인과 추론 3. 개입
이 글은 Causal Inference in Statistics: A Primer의 4장 내용을 기반으로 작성하였습니다. 읽기 전에 인과 추론에서의 그래프 모델 소개를 읽고 오시면 쉽습니다.
pizzathief.oopy.io
Do-calculs에 대해 직관적으로 이해할 수 있도록 쉽게 글을 써주셔서 인과추론 공부에 도움이 되었습니다.
'Statistics' 카테고리의 다른 글
| 인과추론 학습기 - 05. 2SLS와 LATE의 기본 개념 (2) | 2023.06.29 |
|---|---|
| 인과추론 학습기 - 04. 도구변수의 기본 개념 (2) | 2023.05.20 |
| 인과추론 학습기 - 02. 매칭 추정량과 회귀분석 (matching, regression) (1) | 2023.03.11 |
| 인과추론 학습기 - 01. 인과추론의 핵심문제 (선택편의와 교락) (0) | 2023.02.19 |
| 인과추론 학습기 - 00. 왜 인과추론인가? (공부이유, 학습자료) (0) | 2023.01.08 |
