오늘은 인과추론의 핵심요소인 선택편의(Selection bias)와 교락(Confounding)에 대해 써보려고 합니다. 거창하게 두 가지를 쓰기는 했지만, 결론부터 말하면 사실 두 가지는 용어는 달라도 비슷한 내용이라고 말할 수 있습니다.
인과추론의 두 거장, 조슈아 앵그리스트(Joshua Angrist, 2021년 노벨 경제학상 수상)와 주데아 펄(Judea Pearl, 2011년 튜링상 수상)의 표현을 각각 가져온 셈이라, 두 거장(?)의 관점에서 인과추론을 어떻게 바라보는지 위주로 정리해 볼 예정입니다.
인과추론이 어려운 이유
앵그리스트의 표현을 빌리면 '사과 vs 오렌지'를 비교하는 상황에서는 인과성을 추정할 수 없기 때문에 인과추론은 어렵습니다. 이게 무슨 소리인고 하면, "고학력자의 소득이 높을 것이다"라는 명제에서 단순히 학력별 소득을 평균 내서 비교하는 것은 올바른 인과추론이 아니라는 것이죠.
고학력자일 경우, 이미 평균보다 잘 살 가능성이 크고, 이미 가계 소득이 높기 때문에 개인의 소득이 높은 것처럼 보일 수도 있습니다.
진짜로 인과성을 추론하기 위해서는 동일한 한 개인이 일찍 사회활동을 시작했을 경우와, 학업 활동을 계속 했을 때의 소득을 비교할 수 있어야 하겠지만, 멀티 유니버스가 아닌 이상 비교가 불가능하겠죠..

조금 더 간결하게 예시를 들면 한 개인이 '대졸'일 때의 소득과 '고졸'일 때의 소득을 각각 비교할 수 있어야 하는데, '고졸'이라는 선택지를 골라버리면 '대졸'을 골랐을 때의 소득을 알 수 없게 되어버립니다. 내가 고르지 않은 선택지로 얻게 되었을 결과를 잠재적 성과(Potential Outcome)라고 하고, 잠재적 성과와 실제 성과를 비교할 때 우리는 정확한 인과추론을 할 수 있다고 말할 수 있습니다. (이 때의 비교를 사과 vs 사과의 비교라고 할 수 있겠지요.)
위 사실을 고려하지 않고 단순히 고졸자의 임금과 대졸자의 임금을 비교한다면, 당연히 후자의 임금이 높게 나올 것입니다. 앞서 말했듯 여러 외부 요인이 이미 개입한 결과일 수 있을테니까요.
수식으로 표현하면, $Y_i = \beta_0 + \beta_1 * D_i + u_i$ (Y : 소득, D : 대졸/고졸 여부) 라는 회귀 모형으로도 표현할 수 있을텐데요. 우리는 오차항과 결과변수(소득) 간에는 운적인 요소만 작용할 것이라고 기대하지만, 실상 여러 외부 요인들이 오차항($u_i$)에 들어가 버려 오차항과 소득과 강한 연관성(혹은 인과성)을 가지게 되어버립니다.
그래서 극단적으로 고졸/대졸 여부와 소득 간에는 아무 인과성이 없다고 하더라도 오차항과 결과변수가 서로 상관성이 높게 되어(highly correlated) 언뜻 보면 소득/학력 간에 인과성이 있다고 해석될 여지가 있는 것이지요.
오차항과 결과 변수 간에 상관관계가 있는 경우를 우리는 '내생성이 있다(endogeneity)'라고 하고, 내생성이 있을 때 선택편의(Selection Bias)가 발생한다고 이야기합니다.
대졸자의 소득 평균과 고졸자의 소득 평균을 비교한다고 하면 다음과 같은 수식으로 정리가 가능할텐데(D = 1(대졸), D=0 (고졸))
$E(Y_i \mid D_i = 1) - E(Y_i \mid D_i = 0)$
$= (\beta_0 + \beta_1 + E(u_i \mid D_i = 1) - (\beta_0 + E(u_i \mid D_i = 0))$
$= \beta_1 + (E(u_i \mid D_i = 1) - E(u_i \mid D_i = 0))$
고졸인 경우와 대졸인 경우 각각 오차항이 달라지게 되면 $(E(u_i \mid D_i = 1) - E(u_i \mid D_i = 0))$ 이 부분은 0이 아니게 되어버립니다. 실제로 기대한 인과효과($\beta_1$)와 우리가 구하게 된 값이 달라지게 되는데, $(E(u_i \mid D_i = 1) - E(u_i \mid D_i = 0))$ 에 해당하는 부분을 선택편의(selection bias)라고 부르게 됩니다.
내생성과 교란요인
만일, 가계 소득만이 모형에서 빠졌다고 가정한다면 위 경우는 사정이 나은 편입니다. 왜냐하면 모형에 '가계 소득'을 포함시켜주면 되기 때문이죠. 이런 식으로요.
$소득_i = \beta_0 + \beta_1 * 대졸/고졸 여부 + \beta_2* 가계소득 + u_i$
가계소득을 모형에 포함시키면, 오차항에 포함되었던 '가계소득' 영향력은 사라지게 되고, 그러면 선택편의도 사라지게 되기 때문입니다.
그러면 예시를 조금 바꿔서, "스펙이 높을수록 취업이 잘 된다"는 명제가 있고, 어느 정도 상관성이 있어보인다고 가정해 봅시다. (지금에 와서는 이 명제가 맞다고 말할 수 없지만.. 적절한 예시를 떠올리지 못해서 일단 넘어가 봅시다..)
위 명제는 그러면 인과성이 있다고 말할 수 있을까요? 아마 그렇지 못할 것입니다. 스펙과 취업 간에는 일절 관계가 없고, 개인의 능력이 '스펙'과 '취업' 각각 영향을 미친다고 가정해 봅시다. 그러면 스펙이 없더라도 능력이 뛰어난 A 씨는 취업이 가능할 것입니다. 능력이 높을수록 스펙을 쌓을 가능성도 높아지는데, 문제는 우리가 능력을 관찰할 수 없다는 것이지요.
그러면 '능력'에 해당하는 요소는 계속 교차항에 남아 내생성을 야기시킬 것입니다. 이번에는 그래프로 표현해보죠.
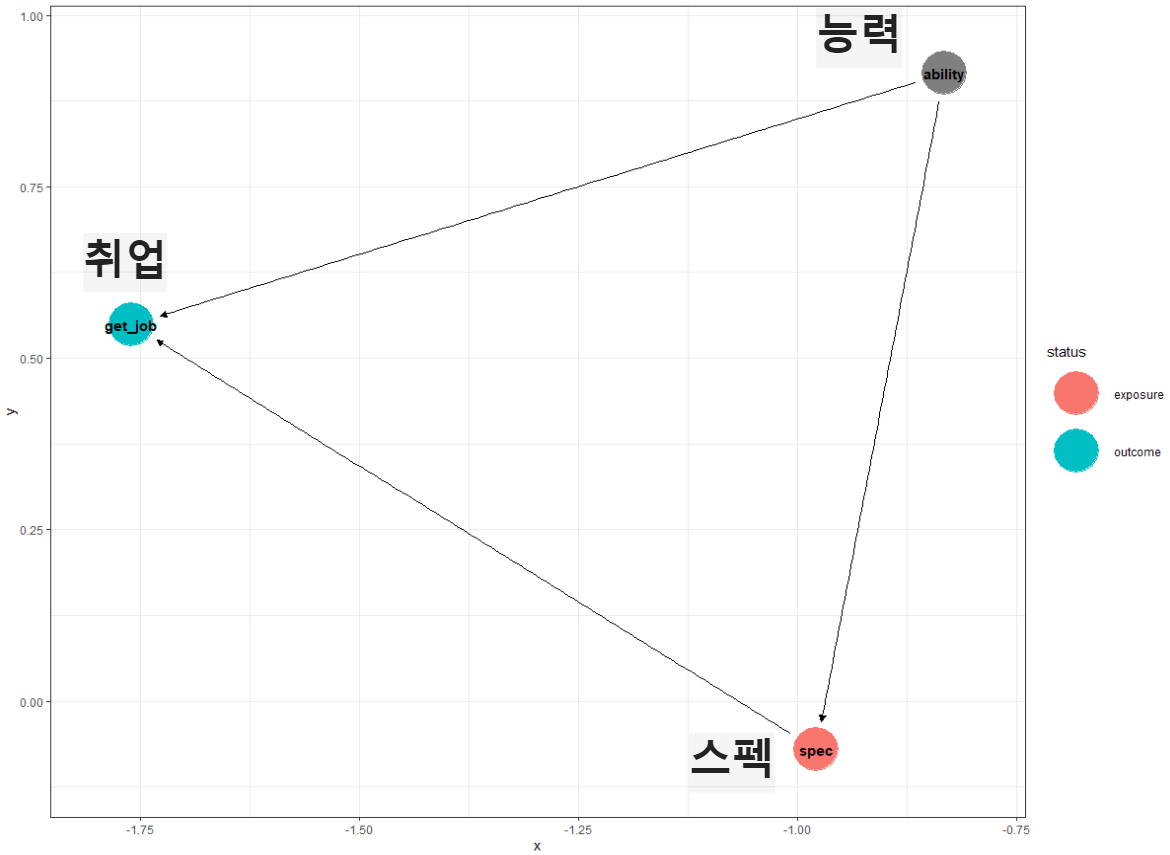
능력이라는 요소는 '스펙'과 '취업'에 모두 영향을 미칩니다. 우리가 알고 싶은 건 '스펙'과 '취업' 간 연관관계인데, 스펙이라는 요소가 내생성을 야기하기 때문에 관계성을 파악하기 어렵습니다. 이 때 '능력'이라는 요소를 교란 변수(Confounding Variable)라고 부를 수 있습니다. 설명변수와 결과변수 둘 다 영향을 미치면서 내생성을 야기하는 요인이죠. 우리가 관찰할 수 있으면 모형에 포함시킬 수 있으니 괜찮은데 문제는 우리가 관찰할 수 없다는 것이죠.
그러면 이걸 어떻게 해결할 수 있을까요?
선택편의/교락을 해결할 수 있는 방법
사실 선택편의와 교락은 앞서 말씀드렸던 두 거장(앵그리스트 교수님/펄 교수님)이 각각 주로 사용하는 용어라고 보시면 될 것 같습니다.
- 선택편의 - 조슈아 앵그리스트
- 교란변수 - 주데아 펄
결국 두 요인 모두 내생성이라는 것과 관련이 있지만 이를 해결하기 위해 강조하는 방식은 약간 차이가 있습니다.
선택편의를 말했단 조슈아 앵그리스트 교수님께서 쓰신 '대체로 해롭지 않은 계량경제학' 책 마지막 권고사항에는 다음과 같은 글귀가 나옵니다. (사실 아직 중간도 못 읽었다는 게 함정이지만)
논리정연한 인과관계 질문들에 대해 회귀분석과 2SLS를 주의 깊게 적용한다면 회귀분석과 2SLS는 거의 언제나 타당한 추정 방법이다.
2SLS는 나중에 블로그에도 정리할 예정이지만 도구변수(Instrumental Variable)의 일종인데, 조슈아 앵그리스트 교수님은 인과추론을 하기 위해서 '회귀분석과 도구변수'를 가장 중요하게 여긴다는 것으로 볼 수 있겠습니다.
반면, 조슈아 펄 교수님은 위와 같은 문제에 대해 do-연산자(do-calculus)를 사용한 조정을 강조합니다.
도구변수가 무엇인지, do 연산자가 무엇인지는 저도 더 공부를 해가면서 기록해 나갈 예정이지만, 간략하게 설명하면
- 도구변수 - 결과 변수(ex.소득, 취업)와 상관관계는 거의 없지만, 관심 대상이 되는 원인 변수와 상관관계가 높은 도구변수를 사용해 내생성을 해결
- do 연산자 - 의도적으로 특정 값을 갖도록 고정(개입) 시키는 방법으로 인과성 추론
이렇게 볼 수 있겠습니다.
다음 글에는 내생성, 회귀분석에 대해 조금 더 자세히 글을 작성해보려 합니다.
참고자료
- Judea Pearl, 의학 및 사회과학 연구를 위한 통계적 인과추론
- Joshua Angrist & Pischke, 대체로 해롭지 않은 계량경제학
'Statistics' 카테고리의 다른 글
| 인과추론 학습기 - 03. 성향점수 매칭(Propensity Score matching) (0) | 2023.04.19 |
|---|---|
| 인과추론 학습기 - 02. 매칭 추정량과 회귀분석 (matching, regression) (1) | 2023.03.11 |
| 인과추론 학습기 - 00. 왜 인과추론인가? (공부이유, 학습자료) (0) | 2023.01.08 |
| ARIMA, SARIMA(계절성 ARIMA) 에 대하여 (2) | 2022.09.28 |
| 단위근 검정, 자기상관검정에 대해 (0) | 2022.09.18 |
