살면서 우리는 일상에서 '매칭'이라는 단어를 많이 사용합니다.
결혼정보회사에서도 등급이 비슷한 남녀를 매칭하여 소개해주고 있고,
게임에서도 비슷한 등급/점수를 가진 사람들끼리 매칭시켜서 플레이를 할 수 있게 해줍니다.
이렇게 우리는 '매칭'이라는 개념에 익숙한데, 인과추론에서 말하는 '매칭' 역시 일상적으로 사용하는 매칭과 크게 다를 것이 없습니다.
1. 매칭이란 무엇인가?

인과추론의 데이터 과학(Youtube)에서 설명을 잘 해주신 걸 가져오기는 가져오기는 했는데,
요는 성질이 비슷하지만, 처치(예. 병원 입원이 건강에 미치는 영향을 본다고 할 때, 입원 여부)에만 차이가 있는 사람들끼리 각각 '매칭'시켜 이 사람들을 비교해서 평균적으로 처치 여부에 따라 종속 변수(관심 변수)에 차이가 있는지 확인하는 개념이라고 볼 수 있겠습니다.
2. 회귀분석과 비교
위의 이미지에서도 '회귀분석'에 대한 언급이 나오기도 하는데, 회귀분석도 '매칭'과 유사한 개념으로 동작합니다.
가령
$Y_i = \alpha + \beta * X_i + \gamma * D_i + \epsilon$
이라는 식이 있다고 하면, $\gamma$라는 회귀 계수가 갖는 의미는 X를 통제한 상태, 즉 X가 동일하다는 가정 하에서 D가 변할 때 Y에 어느 정도 영향을 미치는지를 보여주는 것입니다.
결국 X라는 다른 특성이 동일한 상태에서 D라는 변수가 미치는 영향을 보는 것이므로, 우리는 회귀분석만으로도 충분히 무언가를 '매칭'시킬 수 있게 됩니다.
그러면 회귀분석과 매칭은 왜 용어를 달리 쓰는 건지, 뭐가 어떻게 다른건지 혼란스러워집니다.
2.1 회귀분석과 매칭의 차이점
개인적으로 두 개념을 비교할 때, 비슷한 것을 먼저 찾기보다는 다른 점이 정확히 무엇인지 구분하는 것이 이해가 더 쉬워서 차이가 무엇인지를 파악하는 것을 더 선호하는 편인데.. (TMI)
위의 이미지에서는
Unlike regression, matching doesn't assume a functional form of controls(matching variable) and selection bias.
회귀분석과 달리 매칭은 선택편의와 통제변수의 함수 형태를 가정하지 않는다.
라고 언급하고 있습니다. 즉, 회귀분석은 어쨌든
$Y_i = \alpha + \beta * X_i + \gamma * D_i + \epsilon$ 이런 모양이든,
$Y_i = \alpha + \beta * X_i + \gamma * D_i + \delta * X_i * D_i + \epsilon$ 이런 모양이든 모형의 식을 만들어야 하는데, 매칭은 이런 모양을 가정하지 않는다는 것에서 조금 더 자유로운 방법이라고 볼 수 있는 것입니다.
"대체로 해롭지 않는 계량경제학"에서는
우리의 견해로는 회귀모형은 특수한 종류의 가중 매칭 추정량이다. (p.80)
이라고 말하며 회귀분석과 매칭을 비교하고 있는데요.
매칭은 특정 처치를 받은 사람의 잠재적 결과의 평균 차이를 구하려고 할 때, 처치를 받은 사람의 설명변수의 분포를 이용하여 집계합니다.
조금 수식을 사용하면,
$E(Y_1i - Y_0i | D_i = 1)$ (책의 예시를 따라가면, 군복무 여부에 따른 평균 임금차이) 이 우리가 알고 싶은 값이고, 우리가 관찰할 수 있는 값은 $\delta_x = E(Y_i | X_i, D_i = 1) - E(Y_i | X_i, D_i = 0)$ 입니다.
즉, 비슷비슷한 상태를 가진 사람들 중 처치를 받았냐, 받지 않았냐에 따라 평균 임금 차이를 구하고, 이걸 다시 처치를 받은 사람들의 설명변수 분포를 이용해 가중 평균을 구해서, 결과적으로 처치 효과가 어떤 차이를 만들어냈는지를 보고 싶어하는 것입니다.
대충 개념을 보면,
| 건강점수 | 연령 | 흡연 여부 |
| 70 | 10 | O |
| 80 | 10 | X |
| 85 | 10 | X |
| 90 | 10 | X |
| 30 | 60 | O |
| 40 | 60 | O |
| 50 | 60 | O |
| 60 | 60 | X |
가령 이런 데이터가 있다고 하면,
10대에서 흡연 여부에 따른 건강점수 평균 차이는 -15점, (흡연자 - 비흡연자)
60대에서 흡연 여부에 따른 건강점수 차이는 -20점 (흡연자 - 비흡연자)인데,
흡연 점수에 따른 건강점수 차이를 최종적으로 구할 때 (-15-20) / 2처럼 값을 동일한 가중치로 평균을 내버리는 게 아니라,
흡연자 중 10대와 60대의 분포를 보고 가중평균을 내버리겠다는 것입니다. 즉, 흡연자 4명 중 10대는 1명, 60대는 3명이므로 (-15)*1/4 + (-20)*3/4 이런 식으로 잠재적 평균 차이를 구하겠다는 것에 가깝습니다.
회귀분석은 인과추론의 목적이든, 아니든 어쨌든 의도한 모델링에 따라 LSE(Least Squared Estimator) 방식으로 회귀계수가 구해질텐데, 회귀분석을 사용할 경우 가중평균은 처치 여부의 조건부 분산이 가장 큰 설명변수의 셀에 큰 가중치를 부여합니다.
뭔 소리인고 하면, 10대 / 60대라는 설명변수(공변량)이 주어졌을 때 10대일 때 처치가 들어간 확률은 0.25, 60대일 때 처치 확률은 0.75가 나오게 되는데, 이항분포를 따를 때의 분산은 p(1-p)로 구할 수 있으므로 우리는 10대이든, 60대이든 관계 없이 0.25*0.75의 분산을 얻게 됩니다.
조건부 분산이 같기 때문에 회귀분석을 사용해서 회귀 계수를 구할 때는 -17.5의 결과를 얻게 됩니다.
#R code
y = c(70, 80, 85, 90, 30, 40, 50, 60)
x = c(rep(10, 4), rep(60, 4))
d = c(1, 0, 0, 0, 1, 1, 1, 0)
d<-as.factor(d)
md = lm(y ~ x + d)
summary(md)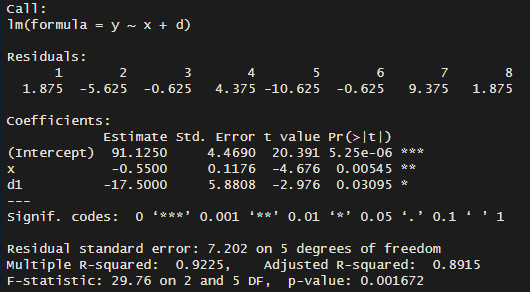
R로 돌려본 결과로도 -17.5라는 회귀 계수를 얻게 됩니다!
즉, 회귀분석과 매칭은
- 회귀분석은 모델링에 대한 fuctional form을 가정해야 하고, 매칭은 이보다는 좀 더 flexible하다.
- 회귀분석은 처치 여부가 주어졌을 때 설명변수의 조건부 분산이 큰 쪽에 가중치가 크게 붙고, 매칭은 처치 여부 별로 설명변수의 분포대로 가중치를 크게 준다는 점에서 차이가 있습니다.
2.2 회귀분석과 매칭의 공통점
위에서부터 언급하기는 했지만, 결국 회귀분석은 특수한 형태의 매칭 추정량입니다.
즉, 두 방법 모두 공변량을 통제한 상태에서 처치 여부가 달라질 때 종속변수(결과변수)에 미치는 영향을 보려고 합니다.
3. 성향점수매칭(Propensity Score Matching)
간략하게 성향점수 매칭에 대해서도 언급해보려고 합니다.
간단히 말하면 성향점수 매칭은 공변량(설명변수)이 비슷한 그룹끼리 처치변수가 배정될 확률(likelihood)을 구하고, 처치된 확률이 비슷한 데이터들을 매칭시키는 방법입니다.
앞서의 매칭 방법에서 설명변수 대신 성향점수(대체로 probit이나 logit 모형을 사용)를 기준으로 매칭하는 것이라고 볼 수 있겠죠.
대체로 해롭지 않은 계량경제학에서는 처치변수가 더미 변수인 경우 회귀모형 대신 매칭을 사용하는 추정 전략을 사용할 수 있다고 합니다.
매칭과 관련해서 검색을 해보면, 설명변수를 이용한 매칭보다는 성향점수 매칭에 대한 이야기가 많이 나오는데.. 다음에는 성향점수 매칭과 역확률 가중치에 대해 글을 작성해보려고 합니다. (과연..?)
'Statistics' 카테고리의 다른 글
| 인과추론 학습기 - 04. 도구변수의 기본 개념 (2) | 2023.05.20 |
|---|---|
| 인과추론 학습기 - 03. 성향점수 매칭(Propensity Score matching) (0) | 2023.04.19 |
| 인과추론 학습기 - 01. 인과추론의 핵심문제 (선택편의와 교락) (0) | 2023.02.19 |
| 인과추론 학습기 - 00. 왜 인과추론인가? (공부이유, 학습자료) (0) | 2023.01.08 |
| ARIMA, SARIMA(계절성 ARIMA) 에 대하여 (2) | 2022.09.28 |
