이번에는 여러 종류의 확률분포에 대한 글을 작성해보려고 합니다. (ex. 이항분포, 정규분포..)
어떤 거창한 의미가 있는 것은 아니고, '개인적으로 공부한 것을 정리해보자!' 하는 취지의 글이기는 해요. 그렇지만 저와 비슷한 상황에 놓인 어떤 누군가에게도 도움이 되길 바라봅니다.
참고로 연속확률분포 / 이산확률분포를 따로 구분하여 작성하지는 않았습니다!
베르누이 분포, 이항분포
통계학에서 가장 기초가 되는 분포라고 할 수 있겠습니다. 옛날에 어떤 자격증 시험(정확히 기억 안남) 보기에 '이항분포', '베르누이 분포'가 동시에 보기로 나와서 갑론을박이 벌어졌던 것 같은 기억이 있는데요.(사실 이것도 정확히 기억 안 남.)
아무튼 요는 같은 뿌리에서 나온 분포이기 때문에 대충 개념만 알면 어떻게든 된다는 말을 하고 싶었습니다.
베르누이 분포
성공(1) 또는 실패(0). 둘 중 하나의 결과값만 얻게 되는 시행(베르누이 시행)에서 1회 시도에서 성공(1)이 나올 확률을 설명하는 분포입니다.
여기서는 모수(parameter)가 성공확률(p)이 되겠지요.
모수
관심이 되는 모집단의 대표값이 정의이기는 한데, 좀 더 직관(?)적으로 표현하면 '이 값만 알면 평균도 구하고, 분산도 구하고, 이 분포에 대한 건 다 알 수 있어!' 라고 말할 수 있겠네요.
이항분포
이항분포는 베르누이 시행을 N번 반복할 때 이 중 내가 원하는 결과값(성공, 1)을 k번 달성하게 될 확률을 설명하는 분포입니다.
가령 SSR 등급을 뽑을 확률이 3%인 가챠를 10번 돌릴 때 SSR등급을 하나도 뽑지 못할 확률을 구하고 싶다거나 하면 이 이항분포를 사용할 수 있겠습니다.
베르누이 분포, 이항분포를 각각 pmf로 정리하면
- 베르누이 분포 : $P(x;p) = p^x*(1-p)^{(1-x)}$
- 이항분포 : $P(x;p) = _nC_kp^x*(1-p)^{(1-x)}$
로 나오게 됩니다.
성공, 실패를 분류하는 문제에서 이항분포를 기본적으로 가정하기 때문에 중요하기도 하지만, 이 분포는 이항분포만큼이나 많이 쓰이는 다른 분포와 연관성이 높기 때문에 더 중요하기도 합니다.
연결되는 분포
- Normal Distribution
- Poisson distribution
- Beta distribution
일단 크게 3개의 분포와의 연관성을 알아보려고 합니다.
정규분포(Normal distribution)
통계학에서 가장 사랑받는(?) 분포죠. 여담이지만 제 블로그 도메인도 정규분포랑 연관성이 있습니다
(CLT의 가호가 함께 하기를..)
해당 분포는
- 평균을 중심으로 왼쪽, 오른쪽이 대칭(symmetric)인 종모양이고,
- 그렇기 때문에 평균과 중앙값(median)이 같고
- 표준편차가 주어지면 데이터가 대략 몇% 확률로 발생 가능한지 표현할 수 있다는 것이
특징일텐데요.
사실 위 문장들은 이 그림 하나로 표현이 되는 것 같습니다.
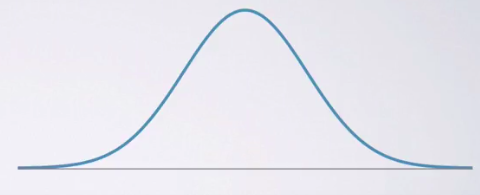
정규분포의 모수(parameter)는 평균과 분산이고, 평균과 분산이 주어지고 정규분포를 따른다는 것을 안다면 사실상 이 모집단에 대해서는 모든 것을 다 안다고 볼 수 있습니다.
가령, 한국인의 평균 몸무게, 그리고 몸무게의 분산을 안다면 Xkg인 나는 한국인의 상위 몇 %인지를 바로 기술할 수 있게 된다는 것이지요.
해당 분포의 pdf는 다음과 같습니다.
- 정규분포 : P(x;$\mu$, $\sigma$) = $\frac{1}{\sqrt2\pi\sigma^2}*e^{\frac{(x-\mu)^2}{\sqrt2\sigma^2}}$
이항분포와의 연결고리
이항분포의 시행횟수를 무한히 늘리게 된다면
- 평균 = 시행횟수*확률
- 분산 = 시행횟수*확률*(1-확률)
인 정규분포를 따르게 됩니다.
따로 증명은 하지 않겠습니다! (대신 참고링크 붙입니다.)
https://bookdown.org/mathemedicine/Stat_book/normal-distribution.html
기초통계 개념정리
This is a basic statistics book written by JSKIM.
bookdown.org
연결되는 분포
- 카이제곱분포 : $X_i$가 정규분포를 따르고, 각각 독립일 때 (iid) $\sum X_i^2$는 카이제곱분포를 따르게 됩니다.
- t분포 : $Z_i$가 정규분포, $X_i$가 카이제곱분포를 따르고 $Z_i$와 $X_i$가 독립일 때, $T = X_i/\sqrt\frac{Z_i}{자유도}$ 는 t분포를 따르게 됩니다.
포아송 분포
단위 시간 안에 원하는 사건이 $\lambda$번 발생할 확률을 표현하는 분포입니다.
포아송 분포에서 모수는 $\lambda$ 입니다.
포아송 분포 역시 이항분포와 연관성이 있는데, 시행횟수(N)가 무한히 많고, 발생확률(p)가 매우 작을 때 N*p 는 $\lambda$에 근사하게 되고, 이항분포 역시 포아송 분포에 근사하게 됩니다.
자세한 증명은 참고 링크를 붙입니다!
https://blog.naver.com/cj3024/221236533062
이항 분포(Binomial distribution) & 포아송 분포(Poisson distribution)
앞서우리는 베르누이 시행에 대해 배웠었습니다. 베르누이 시행이란, 두가지 결과만 가지는 실험을 n번 반...
blog.naver.com
포아송 과정
사실 이항분포가 포아송 분포와 연결되는 것보다 포아송 분포가 다른 분포와 어떻게 연관되는지가 더 중요한데요. 이를 위해서는 포아송 과정에 대한 것을 짚고 넘어가야 합니다.
- 관측을 시작한 시점에 발생횟수는 0이다.
- 겹치지 않는 기간 내에 발생하는 이벤트는 상호 독립이다.(The number of successes in non overlapping intervals are independent)
- 짧은 시간 내 한 사건이 발생할 확률은 시간 길이에 비례한다.
- g(1, h) = $\lambda*h + o(h)$
- 짧은 시간 내 두 개 이상의 사건이 발생할 확률은 0에 가깝다.
- $\sum _2 g(x,h) = o(h)$
가 포아송 과정에 대한 내용인데요. 이러한 포아송 과정 덕분에 우리는 '감마분포'라는 분포를 포아송 분포와 연결지을 수 있게 됩니다.
마찬가지로 자세한 증명은 생략! 하겠지만, 개념만 간략히 짚고 넘어가면
- 포아송 분포 : 일정 시간 내 원하는 사건이 $\lambda$번 발생할 확률분포
- 감마 분포 : 포아송 과정을 따르며, 단위시간 내 사건이 발생할 확률이 $\lambda$일 때 사건이 $\alpha$번째 발생까지 걸리게 되는 대기시간의 확률분포를 의미합니다. Event <-> 대기시간으로 포아송과 감마분포를 대응시킬 수 있게 됩니다.
- 엄밀히는 원하는 사건이 1번 발생하기까지 걸리는 시간을 기술하는 분포가 포아송 분포와 대응된다고 볼 수 있을텐데요. 즉, $\alpha = 1$라면, 감마분포는 지수분포가 되는데, 이 때는 정확하게 Event와 대기시간으로 대응이 가능해집니다.
감마분포
감마함수(Gamma Function)
감마 분포를 이야기하기 위해서는 '감마란 무엇인가?'를 짚고 가야하는데요. 간략하게 설명하면 팩토리얼이 자연수만을 다룰 수 있는데, 이를 복소수 개념까지 확장하도록 만든 것이 Gamma Fuction입니다.
$\Gamma(\alpha)=\int\limits_{0}^{\inf} y^{\alpha -1}e^{-y}\mathrm{d} y$ 모양인데요.
$\Gamma(\alpha) = (\alpha -1)\gamma(\alpha -1)$ 와 같다는 성질을 보입니다.(팩토리얼과 비슷하죠!)
감마 분포는 이러한 감마함수에서 유도되어 pdf는
$P(x;\alpha, \beta)=\frac{1}{\Gamma(\alpha)\beta ^\alpha}x^{\alpha -1}e^{-x/\beta}x$ 를 따르게 됩니다.
이 때 모수는 alpha와 beta인데요. alpha는 shape parameter의 역할을 하고, beta는 scale parameter의 역할을 하게 됩니다.
아까 감마분포는 단위시간 내 사건이 발생할 확률이 $\lambda$일 때 사건이 $\alpha$번째 발생까지 걸리게 되는 대기시간의 확률분포라고 했는데요. 이걸 다시 alpha와 beta의 모양으로 정리하면, alpha = $\alpha$, beta = $\frac{1}{\lambda}$를 모수로 갖는 감마분포를 따른다고 표현할 수 있습니다.
베타분포와의 연결고리
놀랍게도(?) 감마분포 2개를 조합하면 Beta 분포를 도출해낼 수 있습니다.
$X_1$ ~ $\Gamma(\alpha, 1)$, $X_2$ ~ $\Gamma(\beta, 1)$를 따르고, 두 분포가 독립일 때, $X_1 + X_2$는 $\Gamma(\alpha + \beta, 1)$를 따르게 되고, $\frac{X_1}{X_1+X_2}$는 Beta$(\alpha, \beta)$ 분포를 따르게 됩니다.
베타분포
베타분포까지 숨가쁘게 달려왔습니다.
이 분포는 앞서 말했던 이항분포와 연결이 된다고 했는데, 이항분포가 성공과 실패 사건에 대한 확률분포라고 하면, 베타 분포는 성공의 비율을 확률변수로 갖는 분포입니다.
감마분포와 포아송 분포처럼 서로가 대응되는 분포라고 볼 수 있습니다.
베타분포의 pdf는 $P(x; \alpha, \beta) = \frac{\Gamma(\alpha + \beta)}{\Gamma(\alpha)\Gamma(\beta)}x^{\alpha -1}(1-x)^{\beta-1}$를 따르게 됩니다.
이항분포의 pdf $P(x;p) = _nC_kp^x*(1-p)^{(1-x)}$ 와 비슷한 모양을 띄고 있는 것을 확인할 수 있어요.
앞서 Gamma fuction이 팩토리얼을 복소수 개념까지 확장한 것이라고 말씀드렸는데, Gamma Fuction을 팩토리얼로 치환해서 보면 더더욱 이항분포와 비슷하다는 것을 알 수 있습니다.
해당 분포는 베이지안 통계에서 사전확률 분포에서 많이 사용된다고 합니다. 여기서 베이지안에 사전확률분포까지 이야기하면 너무 많은 것을 이야기하게 될 것 같아 이번에는 '베타 분포가 이런 쓰임새가 있구나'까지만 정리하고 넘어가도록 하겠습니다.
(언제가 될 지 모르겠지만..) 다음번에는 베타분포와 함께 베이지안 통계의 기본 개념과 켤레사전분포에 대한 이야기를 진행해보도록 하겠습니다.
'Statistics' 카테고리의 다른 글
| ARIMA, SARIMA(계절성 ARIMA) 에 대하여 (2) | 2022.09.28 |
|---|---|
| 단위근 검정, 자기상관검정에 대해 (0) | 2022.09.18 |
| 주성분 분석(PCA)을 정리해보자! (0) | 2022.06.21 |
| 삶에 적용해 보는 인과분석 (0) | 2022.06.04 |
| 기초 선형대수학 개념 정리 (feat.회귀분석) (0) | 2022.05.26 |
