회귀분석을 공부하다보면 주성분분석(Principal Component Analysis, PCA)에 대한 이야기는 꼭 한 번씩 나오게 됩니다.
막연히 '주성분분석은 차원축소에 사용함', '주성분분석으로 기존 정보를 최대한 확보하는 새로운 변수를 생성함' 등의 내용을 공부하면서 보게 되는데, 오늘은 이 막연한 개념을 정리하는 시간을 가져보려고 합니다.
1. PCA 사용 목적
위에서 간략하게 썼던 것처럼 주성분분석(PCA)은 고차원의 데이터를 저차원의 데이터로 만드는데 사용합니다. 그리고 회귀분석 관점에서는 '다중공선성 문제를 완화'하는데 사용한다고 말합니다.
다중공선성은 설명변수들끼리 서로 상관성이 높을 때, 모형의 회귀계수의 표준오차를 크게 만들어서 모형에 유의한 변수를 찾기 어렵게 만드는 문제를 의미합니다. 이 때, 상관성이 높은 변수들을 축약하고, 몇 개의 변수만을 써서 모형을 만들게 된다면 다중공선성 문제를 해결할 수 있게 됩니다.
또, 회귀분석에 설명변수가 많다면 모형을 해석하는 것이 쉽지 않은데, 이를 몇 개의 변수로 축약하여 해석한다면 몇 개의 변수만으로 단순화한 설명을 할 수 있게 됩니다.
단, 이러한 새로운 변수는 기존 변수들의 선형결합 형태로 만들어지기 때문에 새로운 변수가 이해하기에 직관적인 형태가 아닐 수 있다는 단점이 있습니다.
2. 선형대수 기본 개념 복습
지난번에 선형대수 관련하여 기본 개념을 정리한 링크가 있는데,
https://blessedby-clt.tistory.com/33
기초 선형대수학 개념 정리 (feat.회귀분석)
불과 얼마 전까지만 해도 regression을 가볍게 생각하고 있었습니다. R 콘솔창에 lm(data = data, y ~ X+Z) 만 입력해도 모델링 결과는 쉽게 얻을 수 있었기 때문이지요. 그러나 최근 선형대수학, 회귀분석
blessedby-clt.tistory.com
해당 링크를 참고하셔도 좋을 것 같습니다.
간략하게 정리하면,
- $Ax = \lambda x$ 를 만족하되 lambda의 값이 0이 아니라면, 이 때의 vector를 eigenvector, lambda를 eigenvalue라고 한다.
- $A = A^T$를 만족하는 행렬을 symmetric(대칭)이라고 하고, symmetric한 경우 orthogonal diagonalizable하다. (둘은 필요충분조건)
- orthogonal diagonalizable은 A를 $PDP^T$ (이 때의 P는 orthomornal vector임)로 분해할 수 있다는 뜻이다.
의 3가지로 요약할 수 있을 것 같습니다.
개념을 너무 간략하게 써놔서, 무슨 소리인지 모르겠다 하시는 분들은
- eigenvector, eigenvalue
- symmetric
- diagonalizable
- orthogonal diagonalizable
의 용어를 따로 공부하시는 걸 추천드립니다.
주성분 분석은 설명변수의 공분산행렬(또는 상관계수 행렬을 이용하기도 함)을 이용하여, 해당 변수가 서로 독립(linearly independent)하도록 만드는 새로운 차원을 찾는 것인데,
우리의 재료인 공분산행렬은 (평균이 0이라고 가정하면) $X^TX$ 의 모양으로 나오고, 이는 symmetric 조건을 만족하게 되므로 자연스럽게 orthogonal diagonalizable하다는 것을 알 수 있게 됩니다.
3. 수식 정리
위의 내용을 보다 자세히 풀어보려고 합니다!
- X, Y가 centered 되었다고 가정하면, 우리는 상수항이 없는 모형을 고려할 수 있게 됩니다. 그러면 다음의 식을 얻을 수 있게 됩니다.
- $Y = X \beta + \epsilon$
- 이 경우, X는 centered 되었으므로, X vector의 평균은 0이 되고, 그러면 자연스럽게 X의 공분산 행렬은 $X^TX$ 로 구할 수 있게 됩니다. 위와 같은 형태의 matrix는 symmetric하고, symmetric하면 orthogonal diagonalizable하므로 다음의 식을 가정할 수 있게 됩니다.
- $X^TX = VDV^T$
- 이제, 위의 식을 V = $[V_1, V_2]$, D = diag{$D_1, D_2$} 로 가정하면 $V_1, V_2$를 각각 구성하는 orthonormal한 eigenvector와 Digonal matrix의 대각값으로 eigenvalue를 얻을 수 있게 됩니다.
- 여기서 한 번 더 $Z = XV = [XV_1, XV_2$] = [$Z_1, Z_2$], $\alpha$ = $V^T \beta = \begin{bmatrix} V_1^T \beta \ V_2^T \beta \end{bmatrix} = \begin{bmatrix} \alpha_1 \ \alpha_2 \end{bmatrix}$ 로 가정해 봅시다. 사실 가정이라고 쓰기는 했지만, $Ax = \lambda x$ 를 만족시키는 eigenvector와 eigenvalue를 찾는 거라고 보시면 됩니다.
- 위에서 가정한 식을 활용하면$X \beta = (XV)(V^T \beta) = Z \alpha = Z_1 \alpha_1 + Z_2 \alpha_2$라는 식을 얻을 수 있게 됩니다.
- 이 중 $Z_2$라는 vector를 무시하고 회귀모형을 찾게 되면, (차원축소)
- 즉, Y = $Z_1 \alpha_1 + \epsilon$를 fit하는 모형을 찾게 되면 $\hat \alpha_1 = (Z_1^TZ_1)^{-1}Z_1^TY = (V_1^TX^TXV_1)^{-1}V_1^TX^TY = D_1^{-1}V_1^TX^TY$ 라는 식을 얻을 수 있게 됩니다. ($\because X^TX = VDV^T$)
그러면 우리의 관심사인 회귀계수는 어떻게 구할 수 있을까요? 위에서 구한 값을 그대로 대입하면,
- $\hat \beta^{PCA}$ = $V\begin{bmatrix} \hat\alpha_1 \ 0 \end{bmatrix}$ (아까 $Z_2$ 부분은 버린다고 가정했으므로) = $V_1(D_1^{-1}V_1^TX^TY)$
- $\hat \beta^{LSE}$ = $(X^TX)^{-1}X^TY = (V_1D_1^{-1}V_1^T+V_2D_2^{-1}V_2^T)X^TY$
결과적으로 $\hat \beta^{PCA}$ 와 $\hat \beta^{LSE}$를 비교하면 -$V_2V_2^T\beta$만큼의 차이가 나는 것을 확인할 수 있습니다. 그리고 -$V_2V_2^T\beta$에 해당하는 차이가 작을수록 손실되는 정보양이 작아지게 됩니다.
4. 활용
- 데이터 및 코드는 'R을 이용한 다변량 분석'을 참고했습니다.
rm(list = ls())
# install.packages("HSAUR")
library(HSAUR) ## 데이터 라이브러리
library(car) ## VIF(다중공선성 확인)를 찾기 위한 라이브러리
library(tidyverse)
library(stats)
data("heptathlon")
summary(heptathlon)먼저 데이터를 불러옵니다. 참고로 해당 데이터는 1988년 서울 올림픽 여성 7종 경기에 대한 결과 데이터이며, 각 변수에 대한 설명은 아래와 같습니다.
- hurdles : results 100m hurdles. (110m 허들)
- highjump : results high jump. (높이뛰기)
- shot : results shot. (포환던지기)
- run200m : results 200m race. (200m 달리기)
- longjump : results long jump. (멀리뛰기)
- javelin : results javelin. (창던지기)
- run800m : results 800m race. (800m 달리기)
- score : total score. (종합점수)
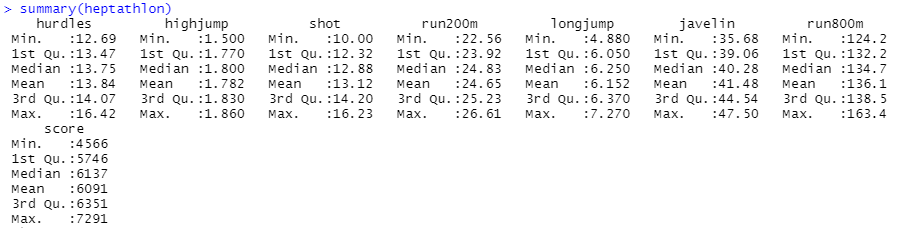
데이터는 위와 같은 요약통계량을 갖고 있습니다.
앞서 주성분분석은 다중공선성 문제를 해결하는데 사용한다고 말했는데, 그러면 일단 주성분분석을 냅다 써보기 전에 갖고 있는 변수로 회귀모형을 돌려보도록 합시다. 항목별 점수로 종합점수를 예측하는 모형인데, 사실 종합점수는 항목별 점수가 고루 높을수록 높아질 것이므로 뻔한 걸 검증하게 될수도 있겠네요..
test_lm <- lm(data = heptathlon, score ~.)
summary(test_lm)
vif(test_lm)
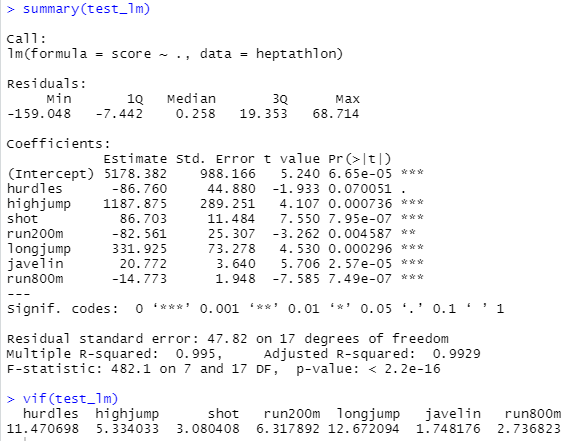
$R^2$ Square가 99%가 넘는 어마무시한 모형입니다. 허들을 제외하면 회귀계수의 p-value는 다 0.05보다 작아 통계적으로 유의한 영향을 보이고 있습니다. 허들, 200m 달리기, 800m 달리기의 회귀계수 부호는 음수인데, 해당 종목은 값이 작을수록 우수한 결과일 것이므로 그렇게 생각하면 크게 특이한 부분은 아닌 것 같네요.
높이뛰기(highjump)의 회귀계수 절대값이 큰 편인데, 결과만 봤을때는 높이뛰기의 영향력이 꽤 큰 것 같습니다.
VIF(다중공선성이 있는지 판별할 때 자주 쓰임, 일반적으로 10 이상이면 다중공선성이 있다고 판단) 결과 다중공선성이 의심된다고 잡힌 변수는 허들(hurdle), 멀리뛰기(longjump)가 있습니다.
이미 모형의 적합성도 좋고, 회귀계수도 대체로 유의하다고 나오는데 주성분분석을 쓰는 게 의미가 있나? 라는 생각이 들기도 했지만(..), 주성분분석을 실습하는 목적이므로 책을 따라서 코드를 더 써보기로 합니다.
# 자료 변형하기 ====
## hurdles, run200m, run800m는 작은 값일수록 좋으므로 자료 변형
heptathlon$hurdles = max(heptathlon$hurdles) - heptathlon$hurdles
heptathlon$run200m = max(heptathlon$run200m) - heptathlon$run200m
heptathlon$run800m = max(heptathlon$run800m) - heptathlon$run800m# 주성분분석 실행하기 ====
library(stats)
hep.data = heptathlon[,-8]
heptathlon.pca = princomp(hep.data, cor = T, scores = T) ## scores : 주성분 점수 출력 옵션 ## cor = T(상관행렬) / cor = F (공분산행렬)princomp 명령어를 입력하면 주성분분석을 돌릴 수 있게 됩니다. 참고로 원데이터의 마지막 컬럼이 종합점수에 해당하는, 즉 종속변수라서 제외해주었습니다.
# 주성분결과 요약 ====
## 결과요약
summary(heptathlon.pca)
## 스크리 그림, 주성분 계수
screeplot(heptathlon.pca, type = "lines", main = "Scree Plot")
heptathlon.pca$loadings[,1:2]
주성분분석을 돌린 summary는 다음과 같습니다. Proportion of Variance는 각 주성분이 어느 정도 분산을 설명하고 있는지를 보여주는데요.
comp1에 해당하는 첫번재 주성분이 전체 분산의 63.7%를 설명하고 있고, 두번째 주성분은 17.06%를 설명하고 있어서 두 개의 주성분을 이용할 경우 전체 분산의 약 80%의 정보를 갖게 됩니다.
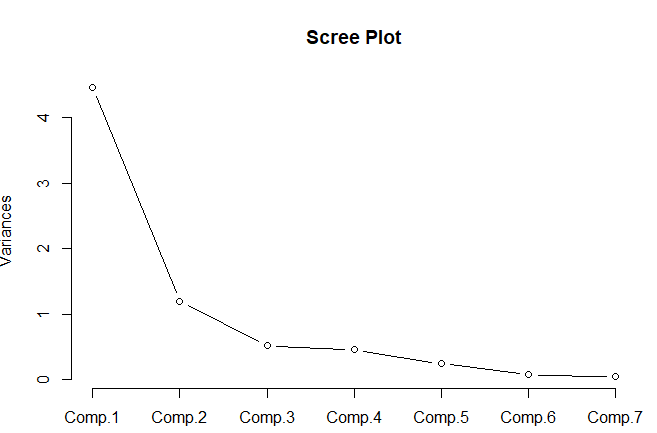
몇 개의 주성분을 사용하는 게 적절한지 Scree Plot을 그려서 확인할 수도 있는데 Variance가 급격하게 감소하다 평평해지는 지점을 기준으로 확인하게 됩니다.
해당 그림에서는 주성분1에서 주성분2까지 급격하게 감소하고, 이후 분산이 감소하는 정도가 매우 작아지기 때문에 스크리 그림을 통해서도 주성분 2개까지를 유효하다고 판단할 수 있습니다.
##주성분점수및 행렬도
heptathlon.pca$scores[,1:2]
biplot(heptathlon.pca, cex = 0.7, col=c("black","red"), main="Biplot")
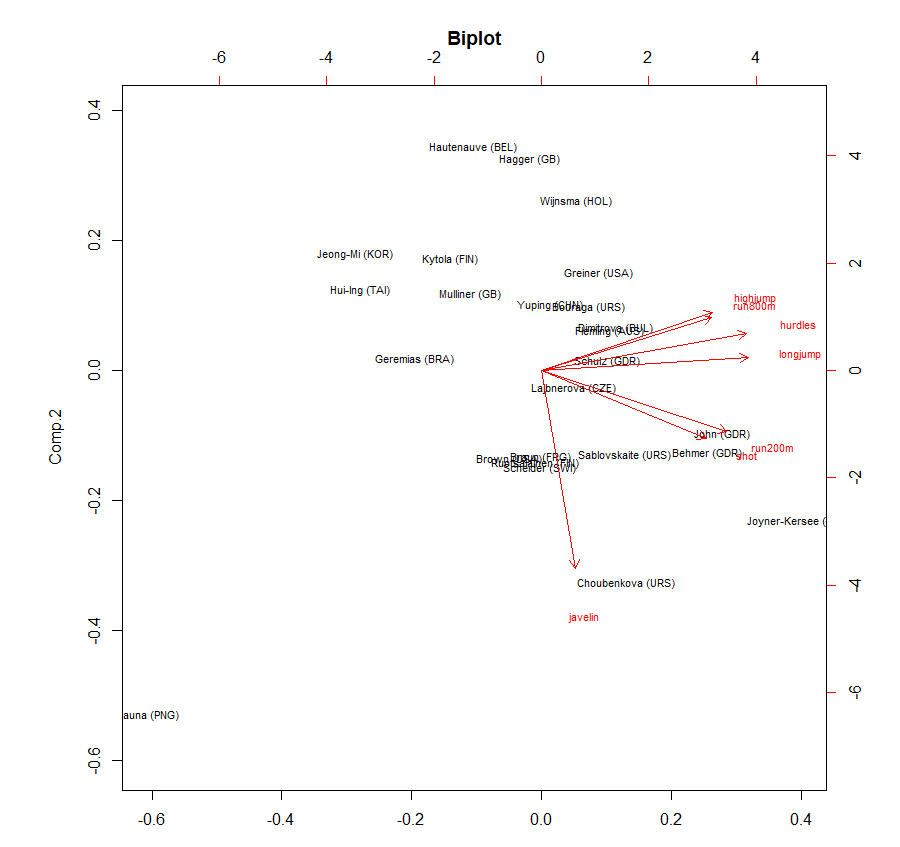
위 코드를 통해 biplot을 그릴 수 있는데, biplot은 record와 주성분과의 관계를 표시한 그래프입니다. 원래의 변수를 기반으로 주성분1, 주성분2을 만들었는데, 이 주성분1, 주성분2를 새로운 축으로 할 때 우리의 record가 어떤 관계를 갖는지 바로 확인할 수 있다는 이점이 있습니다.
javelin(창던지기)를 제외한 나머지 변수들끼리는 상관성이 높은 것을 확인하실 수 있습니다.
마지막으로 PCA로 얻은 주성분으로 회귀모형을 돌리면 어떻게 되는지를 확인해보겠습니다.
heptathlon.pca_new <- heptathlon %>% cbind(., heptathlon.pca$scores[,1:2])
head(heptathlon.pca_new)
test_lm2 <- lm(data = heptathlon.pca_new, score ~ Comp.1 + Comp.2)
summary(test_lm2)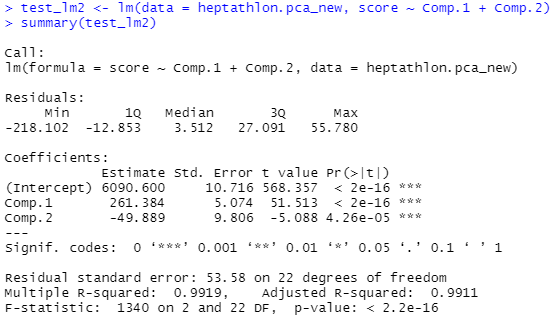
두 개의 주성분으로 앞서와 비슷한 회귀모형의 적합도를 얻게 되었습니다.(R 스퀘어가 비슷해요!)
다만, 변수가 주성분으로 변하면서 모형의 의미를 직관적으로 이해할 수 없게 되었습니다.
<참고링크>
https://darkpgmr.tistory.com/110
[선형대수학 #6] 주성분분석(PCA)의 이해와 활용
주성분 분석, 영어로는 PCA(Principal Component Analysis). 주성분 분석(PCA)은 사람들에게 비교적 널리 알려져 있는 방법으로서, 다른 블로그, 카페 등에 이와 관련된 소개글 또한 굉장히 많다. 그래도 기
darkpgmr.tistory.com
[Machine learning] PCA 주성분분석 (쉽게 설명하는 차원 축소 기법들 총정리 part1) 200803
Index 1. 차원 축소는 왜 하는가? 2. PCA 2.0 기본컨셉 2.1 그림으로 살펴보기 2.2.선형대수학 개념 후려쳐서 2.3 코드로 살펴보기 -------------------------------- (다음 포스팅에서) 3. LDA 4. SVD 1. 차원..
huidea.tistory.com
'Statistics' 카테고리의 다른 글
| 단위근 검정, 자기상관검정에 대해 (0) | 2022.09.18 |
|---|---|
| 통계학에서 자주 활용되는 확률분포에 대해 (0) | 2022.08.19 |
| 삶에 적용해 보는 인과분석 (0) | 2022.06.04 |
| 기초 선형대수학 개념 정리 (feat.회귀분석) (0) | 2022.05.26 |
| 감성 시계열 - 정상성, Random-Walk, ARCH에 대한 감성적 견해 (0) | 2021.12.18 |
회귀분석을 공부하다보면 주성분분석(Principal Component Analysis, PCA)에 대한 이야기는 꼭 한 번씩 나오게 됩니다.
막연히 '주성분분석은 차원축소에 사용함', '주성분분석으로 기존 정보를 최대한 확보하는 새로운 변수를 생성함' 등의 내용을 공부하면서 보게 되는데, 오늘은 이 막연한 개념을 정리하는 시간을 가져보려고 합니다.
1. PCA 사용 목적
위에서 간략하게 썼던 것처럼 주성분분석(PCA)은 고차원의 데이터를 저차원의 데이터로 만드는데 사용합니다. 그리고 회귀분석 관점에서는 '다중공선성 문제를 완화'하는데 사용한다고 말합니다.
다중공선성은 설명변수들끼리 서로 상관성이 높을 때, 모형의 회귀계수의 표준오차를 크게 만들어서 모형에 유의한 변수를 찾기 어렵게 만드는 문제를 의미합니다. 이 때, 상관성이 높은 변수들을 축약하고, 몇 개의 변수만을 써서 모형을 만들게 된다면 다중공선성 문제를 해결할 수 있게 됩니다.
또, 회귀분석에 설명변수가 많다면 모형을 해석하는 것이 쉽지 않은데, 이를 몇 개의 변수로 축약하여 해석한다면 몇 개의 변수만으로 단순화한 설명을 할 수 있게 됩니다.
단, 이러한 새로운 변수는 기존 변수들의 선형결합 형태로 만들어지기 때문에 새로운 변수가 이해하기에 직관적인 형태가 아닐 수 있다는 단점이 있습니다.
2. 선형대수 기본 개념 복습
지난번에 선형대수 관련하여 기본 개념을 정리한 링크가 있는데,
https://blessedby-clt.tistory.com/33
기초 선형대수학 개념 정리 (feat.회귀분석)
불과 얼마 전까지만 해도 regression을 가볍게 생각하고 있었습니다. R 콘솔창에 lm(data = data, y ~ X+Z) 만 입력해도 모델링 결과는 쉽게 얻을 수 있었기 때문이지요. 그러나 최근 선형대수학, 회귀분석
blessedby-clt.tistory.com
해당 링크를 참고하셔도 좋을 것 같습니다.
간략하게 정리하면,
- $Ax = \lambda x$ 를 만족하되 lambda의 값이 0이 아니라면, 이 때의 vector를 eigenvector, lambda를 eigenvalue라고 한다.
- $A = A^T$를 만족하는 행렬을 symmetric(대칭)이라고 하고, symmetric한 경우 orthogonal diagonalizable하다. (둘은 필요충분조건)
- orthogonal diagonalizable은 A를 $PDP^T$ (이 때의 P는 orthomornal vector임)로 분해할 수 있다는 뜻이다.
의 3가지로 요약할 수 있을 것 같습니다.
개념을 너무 간략하게 써놔서, 무슨 소리인지 모르겠다 하시는 분들은
- eigenvector, eigenvalue
- symmetric
- diagonalizable
- orthogonal diagonalizable
의 용어를 따로 공부하시는 걸 추천드립니다.
주성분 분석은 설명변수의 공분산행렬(또는 상관계수 행렬을 이용하기도 함)을 이용하여, 해당 변수가 서로 독립(linearly independent)하도록 만드는 새로운 차원을 찾는 것인데,
우리의 재료인 공분산행렬은 (평균이 0이라고 가정하면) $X^TX$ 의 모양으로 나오고, 이는 symmetric 조건을 만족하게 되므로 자연스럽게 orthogonal diagonalizable하다는 것을 알 수 있게 됩니다.
3. 수식 정리
위의 내용을 보다 자세히 풀어보려고 합니다!
- X, Y가 centered 되었다고 가정하면, 우리는 상수항이 없는 모형을 고려할 수 있게 됩니다. 그러면 다음의 식을 얻을 수 있게 됩니다.
- $Y = X \beta + \epsilon$
- 이 경우, X는 centered 되었으므로, X vector의 평균은 0이 되고, 그러면 자연스럽게 X의 공분산 행렬은 $X^TX$ 로 구할 수 있게 됩니다. 위와 같은 형태의 matrix는 symmetric하고, symmetric하면 orthogonal diagonalizable하므로 다음의 식을 가정할 수 있게 됩니다.
- $X^TX = VDV^T$
- 이제, 위의 식을 V = $[V_1, V_2]$, D = diag{$D_1, D_2$} 로 가정하면 $V_1, V_2$를 각각 구성하는 orthonormal한 eigenvector와 Digonal matrix의 대각값으로 eigenvalue를 얻을 수 있게 됩니다.
- 여기서 한 번 더 $Z = XV = [XV_1, XV_2$] = [$Z_1, Z_2$], $\alpha$ = $V^T \beta = \begin{bmatrix} V_1^T \beta \ V_2^T \beta \end{bmatrix} = \begin{bmatrix} \alpha_1 \ \alpha_2 \end{bmatrix}$ 로 가정해 봅시다. 사실 가정이라고 쓰기는 했지만, $Ax = \lambda x$ 를 만족시키는 eigenvector와 eigenvalue를 찾는 거라고 보시면 됩니다.
- 위에서 가정한 식을 활용하면$X \beta = (XV)(V^T \beta) = Z \alpha = Z_1 \alpha_1 + Z_2 \alpha_2$라는 식을 얻을 수 있게 됩니다.
- 이 중 $Z_2$라는 vector를 무시하고 회귀모형을 찾게 되면, (차원축소)
- 즉, Y = $Z_1 \alpha_1 + \epsilon$를 fit하는 모형을 찾게 되면 $\hat \alpha_1 = (Z_1^TZ_1)^{-1}Z_1^TY = (V_1^TX^TXV_1)^{-1}V_1^TX^TY = D_1^{-1}V_1^TX^TY$ 라는 식을 얻을 수 있게 됩니다. ($\because X^TX = VDV^T$)
그러면 우리의 관심사인 회귀계수는 어떻게 구할 수 있을까요? 위에서 구한 값을 그대로 대입하면,
- $\hat \beta^{PCA}$ = $V\begin{bmatrix} \hat\alpha_1 \ 0 \end{bmatrix}$ (아까 $Z_2$ 부분은 버린다고 가정했으므로) = $V_1(D_1^{-1}V_1^TX^TY)$
- $\hat \beta^{LSE}$ = $(X^TX)^{-1}X^TY = (V_1D_1^{-1}V_1^T+V_2D_2^{-1}V_2^T)X^TY$
결과적으로 $\hat \beta^{PCA}$ 와 $\hat \beta^{LSE}$를 비교하면 -$V_2V_2^T\beta$만큼의 차이가 나는 것을 확인할 수 있습니다. 그리고 -$V_2V_2^T\beta$에 해당하는 차이가 작을수록 손실되는 정보양이 작아지게 됩니다.
4. 활용
- 데이터 및 코드는 'R을 이용한 다변량 분석'을 참고했습니다.
rm(list = ls())
# install.packages("HSAUR")
library(HSAUR) ## 데이터 라이브러리
library(car) ## VIF(다중공선성 확인)를 찾기 위한 라이브러리
library(tidyverse)
library(stats)
data("heptathlon")
summary(heptathlon)먼저 데이터를 불러옵니다. 참고로 해당 데이터는 1988년 서울 올림픽 여성 7종 경기에 대한 결과 데이터이며, 각 변수에 대한 설명은 아래와 같습니다.
- hurdles : results 100m hurdles. (110m 허들)
- highjump : results high jump. (높이뛰기)
- shot : results shot. (포환던지기)
- run200m : results 200m race. (200m 달리기)
- longjump : results long jump. (멀리뛰기)
- javelin : results javelin. (창던지기)
- run800m : results 800m race. (800m 달리기)
- score : total score. (종합점수)

데이터는 위와 같은 요약통계량을 갖고 있습니다.
앞서 주성분분석은 다중공선성 문제를 해결하는데 사용한다고 말했는데, 그러면 일단 주성분분석을 냅다 써보기 전에 갖고 있는 변수로 회귀모형을 돌려보도록 합시다. 항목별 점수로 종합점수를 예측하는 모형인데, 사실 종합점수는 항목별 점수가 고루 높을수록 높아질 것이므로 뻔한 걸 검증하게 될수도 있겠네요..
test_lm <- lm(data = heptathlon, score ~.)
summary(test_lm)
vif(test_lm)

$R^2$ Square가 99%가 넘는 어마무시한 모형입니다. 허들을 제외하면 회귀계수의 p-value는 다 0.05보다 작아 통계적으로 유의한 영향을 보이고 있습니다. 허들, 200m 달리기, 800m 달리기의 회귀계수 부호는 음수인데, 해당 종목은 값이 작을수록 우수한 결과일 것이므로 그렇게 생각하면 크게 특이한 부분은 아닌 것 같네요.
높이뛰기(highjump)의 회귀계수 절대값이 큰 편인데, 결과만 봤을때는 높이뛰기의 영향력이 꽤 큰 것 같습니다.
VIF(다중공선성이 있는지 판별할 때 자주 쓰임, 일반적으로 10 이상이면 다중공선성이 있다고 판단) 결과 다중공선성이 의심된다고 잡힌 변수는 허들(hurdle), 멀리뛰기(longjump)가 있습니다.
이미 모형의 적합성도 좋고, 회귀계수도 대체로 유의하다고 나오는데 주성분분석을 쓰는 게 의미가 있나? 라는 생각이 들기도 했지만(..), 주성분분석을 실습하는 목적이므로 책을 따라서 코드를 더 써보기로 합니다.
# 자료 변형하기 ====
## hurdles, run200m, run800m는 작은 값일수록 좋으므로 자료 변형
heptathlon$hurdles = max(heptathlon$hurdles) - heptathlon$hurdles
heptathlon$run200m = max(heptathlon$run200m) - heptathlon$run200m
heptathlon$run800m = max(heptathlon$run800m) - heptathlon$run800m# 주성분분석 실행하기 ====
library(stats)
hep.data = heptathlon[,-8]
heptathlon.pca = princomp(hep.data, cor = T, scores = T) ## scores : 주성분 점수 출력 옵션 ## cor = T(상관행렬) / cor = F (공분산행렬)princomp 명령어를 입력하면 주성분분석을 돌릴 수 있게 됩니다. 참고로 원데이터의 마지막 컬럼이 종합점수에 해당하는, 즉 종속변수라서 제외해주었습니다.
# 주성분결과 요약 ====
## 결과요약
summary(heptathlon.pca)
## 스크리 그림, 주성분 계수
screeplot(heptathlon.pca, type = "lines", main = "Scree Plot")
heptathlon.pca$loadings[,1:2]
주성분분석을 돌린 summary는 다음과 같습니다. Proportion of Variance는 각 주성분이 어느 정도 분산을 설명하고 있는지를 보여주는데요.
comp1에 해당하는 첫번재 주성분이 전체 분산의 63.7%를 설명하고 있고, 두번째 주성분은 17.06%를 설명하고 있어서 두 개의 주성분을 이용할 경우 전체 분산의 약 80%의 정보를 갖게 됩니다.

몇 개의 주성분을 사용하는 게 적절한지 Scree Plot을 그려서 확인할 수도 있는데 Variance가 급격하게 감소하다 평평해지는 지점을 기준으로 확인하게 됩니다.
해당 그림에서는 주성분1에서 주성분2까지 급격하게 감소하고, 이후 분산이 감소하는 정도가 매우 작아지기 때문에 스크리 그림을 통해서도 주성분 2개까지를 유효하다고 판단할 수 있습니다.
##주성분점수및 행렬도
heptathlon.pca$scores[,1:2]
biplot(heptathlon.pca, cex = 0.7, col=c("black","red"), main="Biplot")

위 코드를 통해 biplot을 그릴 수 있는데, biplot은 record와 주성분과의 관계를 표시한 그래프입니다. 원래의 변수를 기반으로 주성분1, 주성분2을 만들었는데, 이 주성분1, 주성분2를 새로운 축으로 할 때 우리의 record가 어떤 관계를 갖는지 바로 확인할 수 있다는 이점이 있습니다.
javelin(창던지기)를 제외한 나머지 변수들끼리는 상관성이 높은 것을 확인하실 수 있습니다.
마지막으로 PCA로 얻은 주성분으로 회귀모형을 돌리면 어떻게 되는지를 확인해보겠습니다.
heptathlon.pca_new <- heptathlon %>% cbind(., heptathlon.pca$scores[,1:2])
head(heptathlon.pca_new)
test_lm2 <- lm(data = heptathlon.pca_new, score ~ Comp.1 + Comp.2)
summary(test_lm2)
두 개의 주성분으로 앞서와 비슷한 회귀모형의 적합도를 얻게 되었습니다.(R 스퀘어가 비슷해요!)
다만, 변수가 주성분으로 변하면서 모형의 의미를 직관적으로 이해할 수 없게 되었습니다.
<참고링크>
https://darkpgmr.tistory.com/110
[선형대수학 #6] 주성분분석(PCA)의 이해와 활용
주성분 분석, 영어로는 PCA(Principal Component Analysis). 주성분 분석(PCA)은 사람들에게 비교적 널리 알려져 있는 방법으로서, 다른 블로그, 카페 등에 이와 관련된 소개글 또한 굉장히 많다. 그래도 기
darkpgmr.tistory.com
[Machine learning] PCA 주성분분석 (쉽게 설명하는 차원 축소 기법들 총정리 part1) 200803
Index 1. 차원 축소는 왜 하는가? 2. PCA 2.0 기본컨셉 2.1 그림으로 살펴보기 2.2.선형대수학 개념 후려쳐서 2.3 코드로 살펴보기 -------------------------------- (다음 포스팅에서) 3. LDA 4. SVD 1. 차원..
huidea.tistory.com
'Statistics' 카테고리의 다른 글
| 단위근 검정, 자기상관검정에 대해 (0) | 2022.09.18 |
|---|---|
| 통계학에서 자주 활용되는 확률분포에 대해 (0) | 2022.08.19 |
| 삶에 적용해 보는 인과분석 (0) | 2022.06.04 |
| 기초 선형대수학 개념 정리 (feat.회귀분석) (0) | 2022.05.26 |
| 감성 시계열 - 정상성, Random-Walk, ARCH에 대한 감성적 견해 (0) | 2021.12.18 |
