불과 얼마 전까지만 해도 regression을 가볍게 생각하고 있었습니다. R 콘솔창에 lm(data = data, y ~ X+Z) 만 입력해도 모델링 결과는 쉽게 얻을 수 있었기 때문이지요.
그러나 최근 선형대수학, 회귀분석, 인과분석을 공부하면서 '굉장히 얕은 수준만을 맛보고 안다고 착각하고 있었구나' 하고 깨닫는 순간이 있었고, 기초를 다진다는 느낌으로 관련 내용을 정리해보는 시간을 갖기로 마음먹었습니다.
그리고 이를 위한 첫번째 스텝으로
- 선형대수에서 꼭 알아야 하는 기초 개념
(자세한 내용은 맨 하단 참고링크를 따라가시는 것을 추천드려요! 😃) - 기초 개념이 어떻게 회귀분석과 연결되는지
를 나름의 견해를 담아 정리해보았습니다.
linearly independent
해당 개념은 선형대수학 책을 펼치면 가장 초반에 나오는 내용으로, 쉽다면 쉽지만 뒷단에 나오는 개념들의 기둥이 되므로 매우 중요한 부분입니다!
기본 개념
$R^n$ space에서 ${x_1, x_2, x_3... x_p}$ 의 벡터들이 다음의 조건을 만족할 때 linearly independent하다고 정의합니다.
- $c_1*x_1 + c_2*x_2 + ... + c_p*x_p = 0$
- $c_1 = c_2 = ... = c_p = 0$
즉, 벡터들의 선형결합을 0벡터로 만드는 상수항은 모두 0이어야만 한다는 뜻입니다. 반대로 $c_1, c_2,...,c_p$의 해가 단 하나라도 0이 아니게 될 경우 선형종속(linearly dependent)이 됩니다.
linearly dependent한 경우, 최소한 하나의 vector는 다른 vector들의 선형결합(linear combination)으로 표현이 됩니다!
회귀분석에 개념 적용
먼저 회귀분석에 해당 개념이 어떻게 연결되는지를 작성하기 앞서, 회귀분석에 대한 몇 가지 가정을 짚고 가야할 것 같습니다!
- 오차항의 독립성
- 오차항의 정규성
- 선형성
- 등분산성
- No multicollinearity (다중공선성이 없을 것)
- (한 가지 덧붙이면 내생성이 없을 것(외생성) 조건이 있는데, 이는 인과분석에서 중요하게 생각하는 개념입니다!)
대략 이 정도를 가정하는데 이 중, 앞서 말씀드린 linearly independent 조건은 다중공선성과 대응된다고 볼 수 있을 것 같습니다.
예시를 간략하게 들면,
- $X_1, X_2, .., X_p$ 의 변수를 가진 회귀식이 있다고 할 때, 다음 2개의 변수가 단지 가격을 단위 별로 다르게 했을 뿐이라고 가정($X_1$(원화), $X_2$(달러))
($X_1$ = $-X_2$ 의 등식이 성립되어 linearly dependence하게 됩니다.) - 회귀분석 관점에서도 $X_1$(원화), $X_2$(달러)의 변수가 갖고 있는 정보가 동일하므로 Multicollinearlity가 성립됩니다.
- 이렇게 변수 간 다중공선성을 갖게 된다면, 회귀계수(coefficient)의 분산이 커지게 됩니다!
- 아래에서 다시 언급할 예정이기는 하지만, 회귀계수의 OLS는 아래 식으로 구해지게 되는데요.
- $\hat{b}$ = $(X^TX)^{-1}(X^TY)$
- X vector가 linearly dependence 하다면 $(X^TX)^{-1}$를 구할 수 없게 되고, 즉 분산은 무한대에 가까워지므로, 실제로 유의한 회귀계수를 유의하지 않다고 판단할 수 있게 됩니다.
- 단, 다중공선성이 있더라도 불편성(unbiasedness) 조건은 만족하고, 오히려 다중공선성을 없애기 위해 변수를 잘못 통제하게 될 경우, 불편성 조건을 만족하지 못하는 사태가 벌어질 수 있기 때문에 주의하시는 것이 좋겠습니다!
Orthogonal
기본 개념
- $v_1 \cdot v_2$ = 0 의 식이 성립할 때 $v_1, v_2$의 벡터는 orthogonal하다고 말합니다.
orthogonal basis
- $R^n$의 부분공간인 W의 basis를 이루는 벡터들이 서로 orthogonal하다면 해당 vector들은 W의 orthogonal basis라고 말할 수 있게 되고,
- $u_1, u_2, ..., u_p$의 vector가 orthogonal basis일 때, $c_j$ = $y \cdot u_j \over u_j \cdot u_j$ 의 수식을 만족하게 됩니다.
projection
- 예를 들어 a벡터를 b벡터에 projection한다고 가정해보죠.
- a벡터를 b벡터에 projection한다는 것은 a벡터를 b벡터 방향을 갖는 벡터와, b벡터와 직교(orthogonal)하는 벡터로 쪼개고, 이 중 b벡터 방향과 동일한 벡터를 a벡터의 정사영(orthogonal projection on a onto b)이라고 합니다.
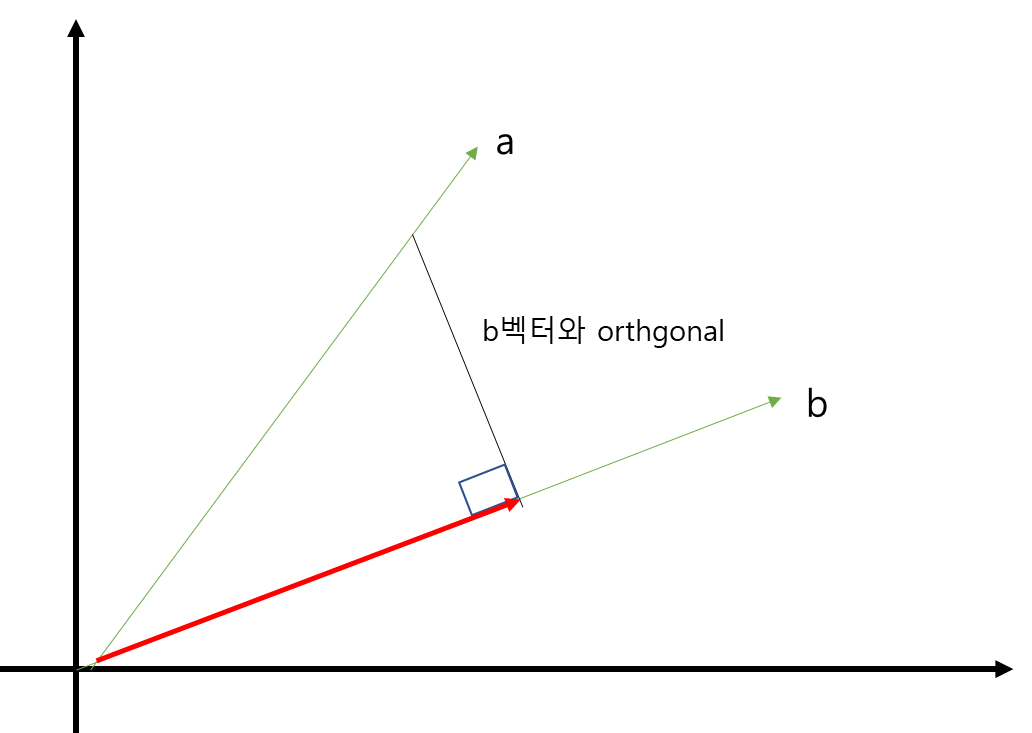
- 해당 개념을 기반으로 회귀분석의 LSE(Least Square Estimation)를 구하게 됩니다.
회귀분석에 개념 적용
- 데이터는 변수 개수가 레코드 개수보다 적기 때문에, 방정식의 해를 구할 수 없는 것이 일반적입니다.
- (구해야 하는 값은 x, y 2개 뿐인데 만족해야 하는 조건이 5개라면, x,y에 해당하는 값을 구할 수 없을테니까요.)
- 그렇지만, 종속변수에 해당하는 벡터를 projection 시켜서, 방정식의 해의 근사값을 찾는 것은 가능할 것입니다!
- 방정식의 해(회귀분석에서는 회귀계수의 집합이 해가 됩니다!)를 어떻게 구할 수 있는지는 하단 이미지로 정리했고,
- 대충(?) 요약하면, y벡터를 projection 시켰을 때, 이와 직교(orthogonal)하는 벡터를 찾고, 해당 벡터는 X벡터의 Span과도 orthogonal할 것이므로 이런 orthogonal한 관계성을 고려해가면서 LSE를 구한다고 보시면 될 것 같아요.
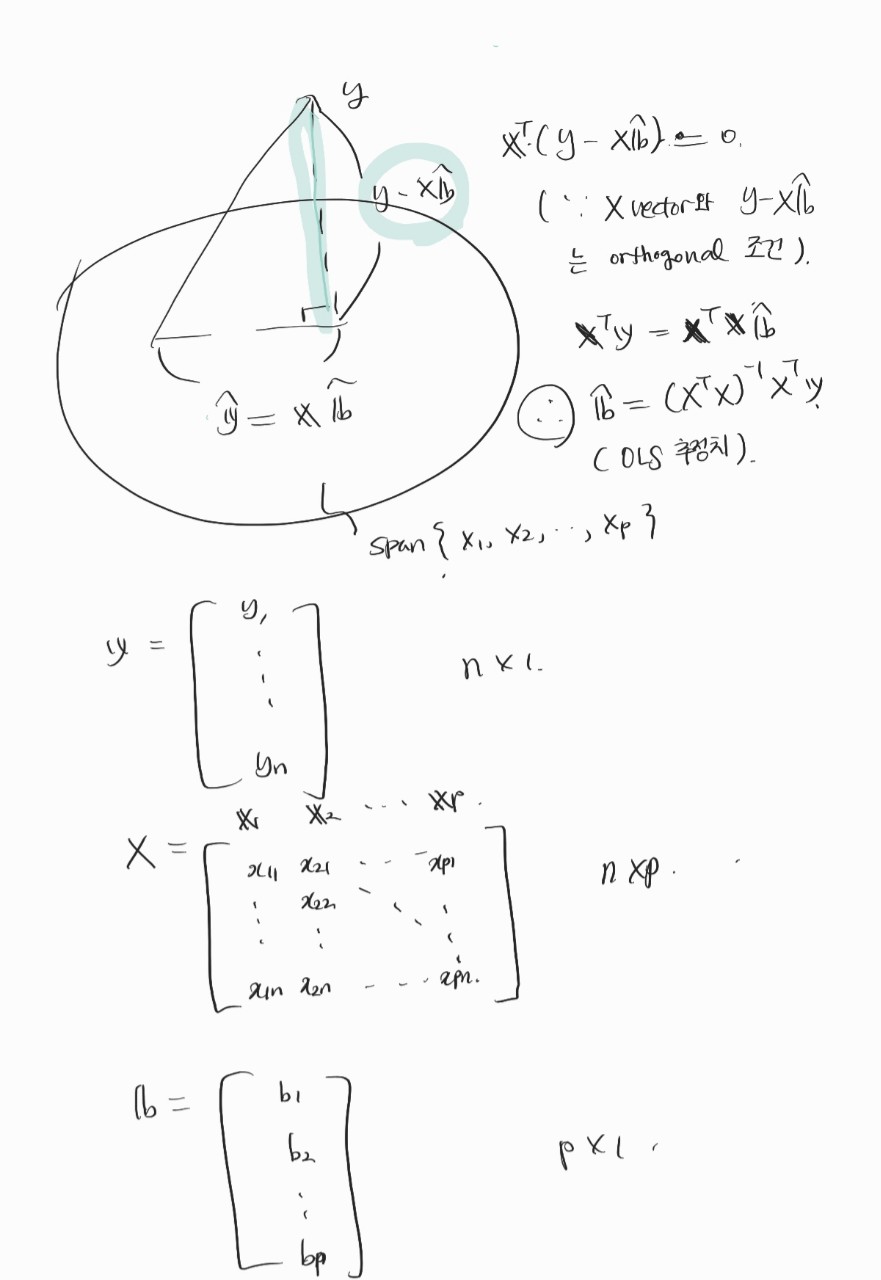
Eigenvalues and Eigenvectors
다음으로는 회귀분석의 꽃(?)인 eigenvalue와 eigenvector에 대해서 이야기해보려고 합니다. PCA를 이야기할 때 빼놓지 않고 등장하는 개념이기도 해서 알아두면 큰 도움이 될 거라고 생각해요! (사실 저도 맨날 까먹고 잘 모르지만..)
기본 개념
$Ax = \lambda x$ 을 만족하는 x벡터를 eigenvector라고 하고, x벡터의 해가 nontrivial하다면(x벡터가 0일때만 다음 식이 성립한다면 trivial) 이 때의 해를 eigenvalue라고 합니다.
관련해서 몇 가지 개념을 같이 알아두면 좋은데......
diagonalization
- $A = PDP^{-1}$ 를 만족한다면 A는 diagonalizable하다고 말하고,
- diagonalizable하다면, D(대각행렬)의 entry는 eigenvalue를 갖게 되고,
- A는 n개의 linearly independent한 eigenvector를 가지게 됩니다. 그리고 P의 column이 A의 eigenvector가 됩니다.
symmetric
- $A^T = A^{-1}$한 조건을 만족하게 되면 A 행렬은 symmetric하다고 말합니다.
- A 행렬이 symmetric하면 서로 다른 고유공간(eigenspace)에 있는 eigenvector는 서로 orthogonal하며,
- orthogonal diagoanlizable한 특성을 갖게 됩니다.
orthogonal diagonalizable
- $A = PDP^T = PDP^{-1}$ 의 등식을 만족하는 경우, orthogonal diagonalizable하다고 말하며, 이 조건을 만족하는 A행렬은 symmetric합니다.
- symmetric조건과 orthogonal diagonalizable 조건은 필요충분조건(if and only if)입니다.
회귀분석에 적용
diagonalizable하면 n개의 독립적인 eigenvector와 eigenvalue를 무조건 찾을 수 있다는 장점이 있고, 특히 행렬이 symmetric하다면 orthogonal diagonalizable이 보장되기 때문에 symmetric한 조건은 굉장히 매력적이라고 할 수 있습니다.
실제 symmetric한 행렬을 많이 사용할 일이 있을까 싶기는 하지만, 다행히 회귀분석에서 사용하는 우리의 공분산 행렬은(covariance matrix) symmetric하기 때문에 orthogonal diagonalizable이 가능하고, n개의 linearly independent한 eigenvector를 찾을 수 있게 되어서 eigenvector를 쉽게 찾을 수 있습니다!
공분산 행렬이 대칭이라는 개념을 기반으로 차원 축소에 PCA를 사용하게 되는데, 이 부분은 다음에 작성하여 정리하는 것으로 하겠습니다!
참고 링크
https://soohee410.github.io/orthogonal_projection
[선형대수] Orthogonal Projection
[선형대수] Orthogonal Projection Published Jan 18, 2020 <!-- --> 안녕하세요! 이번 포스트에서는 정사영(Orthogonal Projection) 에 대해 제가 배웠던 내용을 정리하고자 합니다. 바로 시작하겠습니다 😊 1. 정사영
soohee410.github.io
https://elementary-physics.tistory.com/21
(선형대수학) 3.1 Eigenvalue, Eigenvector, Eigenspace
(선형대수학) 2.5 Representations of Linear Transformations에서 보았듯이, Linear operator는 vector space의 basis가 주어지면 matrix로 표현될 수 있다. Basis를 어떻게 선택하느냐에 따라서 계산에 편리한 m..
elementary-physics.tistory.com
https://angeloyeo.github.io/2019/07/27/PCA.html
주성분 분석(PCA) - 공돌이의 수학정리노트
angeloyeo.github.io
'Statistics' 카테고리의 다른 글
| 주성분 분석(PCA)을 정리해보자! (0) | 2022.06.21 |
|---|---|
| 삶에 적용해 보는 인과분석 (0) | 2022.06.04 |
| 감성 시계열 - 정상성, Random-Walk, ARCH에 대한 감성적 견해 (0) | 2021.12.18 |
| 수리통계학 - EM 알고리즘 (0) | 2021.09.17 |
| 수리통계학 - MLE와 MVUE에 대하여 (2) | 2021.08.28 |
