시계열 분석을 오랜만에 공부하면서, '단위근 검정', '자기상관 검정' 등 시계열 분석에 필요한 검정 방법에 대해서도 다시 공부하게 되었습니다.
이전에 개념을 제대로 못 잡은 탓인지 몰라도 몇 가지 의문이 들었었는데
- 단위근 검정 = 정상성을 확인하기 위한 검정이고, 정상성은 약정상성 기준으로 평균, 분산이 일정하고 자기상관이 시차에만 의존하는 경우
- 자기상관 검정 = 잔차의 자기상관이 있는지 확인하기 위한 검정
- 단위근 검정에서 말하는 자기상관과 자기상관검정에서 말하는 자기상관이 뭐가 다르지? 비슷한건가?
- 비슷한 거면 자기상관 검정 왜 함?
의 흐름으로 궁금증이 들었습니다.
기존에 알고 있다고 생각한 개념이 제대로 잡히지 않은 것 같아, 이번 기회에 정상성과 단위근검정, 자기상관검정 개념을 정리해보려고 합니다.
정상성
시계열을 이야기할 때 빼놓지 않고 이야기할 수밖에 없는 개념이라고 생각합니다. 정상성을 만족해야 하는 이유가 무엇인지 직관적으로 이해해야 검정에 대해서도 이해할 수 밖에 없기 때문에 정상성이 무엇인지, 정상성이 왜 중요한지에 대해 정리를 해보려고 합니다.
먼저 시계열 데이터(Time Series data)의 특징적인 부분에 대해서 이야기해보면, x축이 time(시간)이라는 것입니다.
이게 무슨 말장난 같은 이야기인가 싶겠지만, 사실 제일 중요한 부분이기도 합니다.
횡단면 데이터(Cross-sectional data)를 생각해보죠.
대한민국 성인 남성, 여성의 키 분포를 볼거야! 라고 했을 때, 저 하나 쯤의 데이터가 사라져도 원하는 통계량을 확인할 수 있을 겁니다. Sample이 엄청 많다는 가정 하에서는요.
WLLN(대수의 법칙), CLT(중심극한정리) 등을 활용하면 평균이나 분산의 추정치를 구할 수 있을 거에요.
그러나 시계열 데이터에서 특정 날짜 데이터에 결손이 생기게 되면 다른 샘플로 메꿀 수 있을까요? 혹은 2022년 9월까지의 데이터로 10월의 데이터를 예측할 수 있을까요?
위의 목표를 달성하기 위해서는 전제가 필요합니다.
오늘의 통계량이 내일의 통계량에도 어느 정도 적용 가능할 것이라는 것 말이죠.
평균과 분산이 일정하지 않고 여기저기 튀는 상황이라면, 저는 특정날짜 데이터의 결손이 생기더라도 다른 날짜 데이터로 보간을 할 수 없을 것이고 미래의 날도 어차피 오늘의 데이터로 예측이 불가능한 상황이기 때문에 예측이 아니라 나만의 토속신앙을 활용하는 편이 마음이 더 편할지도 모를 거에요.
그러나 장기적으로 평균은 일정하고, 비록 error term(내가 예측 못하는 shock)가 있더라도 그 분산이 일정하다는 믿음이 있다면, 결손치 보간도 미래치 예측도 가능할 겁니다!
그리고 정상성의 특징을 한 가지 더 말하자면 $Y_t$시점과 $Y_{t+h}$ 시점의 공분산은 h에만 의존하고 t에는 의존하지 않아야 한다는 것입니다. 즉, 오늘의 영향이 5일 후에 미치는 영향과 내일의 영향이 (오늘로부터) 6일 후 미치는 영향이 일정해야 한다는 가정입니다. 만일 공분산이 t에 의존하게 된다면 결국 특정 일자의 영향이 중요하다는 뜻이 됩니다.
특정 일자의 영향력이 중요하게 되면, 마찬가지로 미래 시점의 데이터를 예측하기 어렵기 때문에 $Y_t$시점과 $Y_{t+h}$ 시점의 공분산은 h에만 의존해야 합니다.
결국 정상성을 만족해야만 우리는 시계열 데이터를 통해 미래를 예측할 수 있게 됩니다.
그러나 현실의 데이터는 정상성이라는 것을 만족하지 않는 경우가 많습니다.
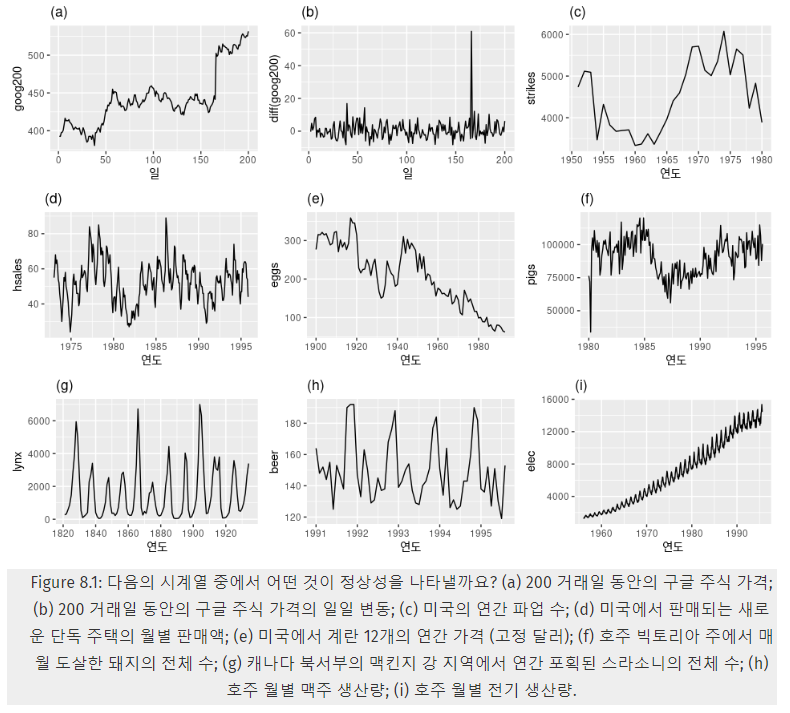
위의 이미지에서 정상성을 만족하는 그래프는 (b) 정도로만 보입니다. 현실의 데이터는 (d)처럼 계절성(특정 주기마다 데이터가 증가하거나 감소)을 만족하거나, (a)나 (e)처럼 증가/감소 추세를 보이는 데이터가 많습니다.
이런 경우에는 TSP(deTrend Stationary Process : 추세 제거) 또는 DSP(Difference Stationary Process : 차분) 방법을 사용하는데, 단순히 추세만 제거해도 되는 경우에는 TSP를 사용해도 괜찮지만, Unit Root가 존재하는 경우에는 차분을 해야 합니다.
그리고 Unit Root가 존재하는지를 확인하는 방법이 단위근 검정입니다.
단위근 검정
위에서 정상성이 중요한 이유, 그리고 짤막하게 단위근(Unit Root)에 대해서 이야기했습니다. 그러면 Unit Root는 무엇일까요?
이를 설명하기 위해서는 AR 모형이나 중간에 많은 과정의 설명들이 필요한데, 이 설명들을 제외하고(사실 제외하면 안 되지만) 최대한 직관적으로 설명하면 오늘의 영향력이 미래에 어느 정도 영향을 미치는지를 결정하는 모수(parameter)가 단위근이라고 볼 수 있습니다. 이 모수가 -1보다 크거나 1보다 작은 경우에는 시간이 지나고 미래에는 특정 일자의 영향력이 사라지지만, 이 모수가 1인 경우에는 오늘의 영향력이 내일에 영구히 영향을 미칠 수 있게 된다는 뜻입니다.
오늘의 영향력이 미래에 영구히 영향을 미칠 수 있게 된다면 그 데이터는 더이상 정상성을 만족하지 못하게 됩니다.(Non-Stationary)
하지만 차분을 한 데이터($Y_t - Y_{t-1} = \Delta Y$)는 정상성을 만족하게 됩니다.
예를 들어 $Y_t = Y_{t-1} + e_t (where, e_t \sim iid (0, {\sigma}^2)) $ 라는 모델이 있다고 하면, 오늘의 데이터는 어제의 데이터의 영향력이 계속 누적되지만, 차분을 한다면 $Y_t - Y_{t-1} = \Delta Y = e_t$의 모양이 나오게 되고, $e_t$는 정상성을 만족하는 데이터이기 때문에 우리는 차분만으로 비정상 데이터를 쉽게 정상 데이터로 바꿀 수 있게 되는 것입니다.
단위근이 있다는 것을 안다 = 차분을 하면 어느 정도 해결을 할 수 있다 라는 주요한 키포인트를 알 수 있게 되는 것이므로, 그래서 처음 데이터를 분석하기 전에 단위근 검정을 해보는 것 같습니다.
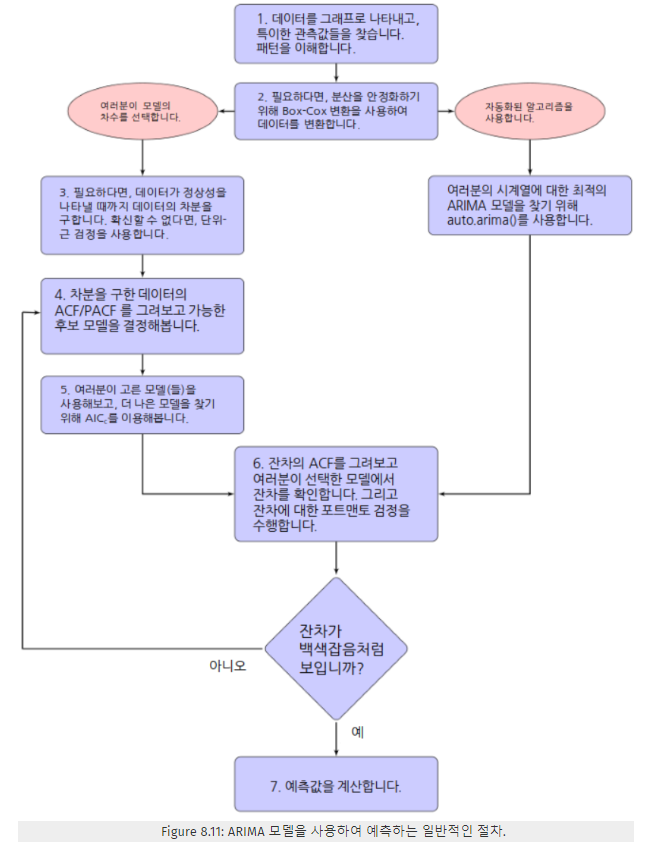
ARIMA 모델을 사용하는 일반적인 절차에서 3번 과정이 단위근 검정에 해당하는 절차라고 볼 수 있겠네요.
그리고 이러한 단위근 검정의 대표적인 검정 방법이 ADF(Argumented Dickey-Fuller test)입니다.
library(forecast)
library(tidyverse)
library(fpp2) # 데이터 로드용
library(tseries) # adf test를 하기 위한 라이브러리
data(goog200)
# goog200 원본 데이터
autoplot(goog200)
ggtsdisplay(goog200)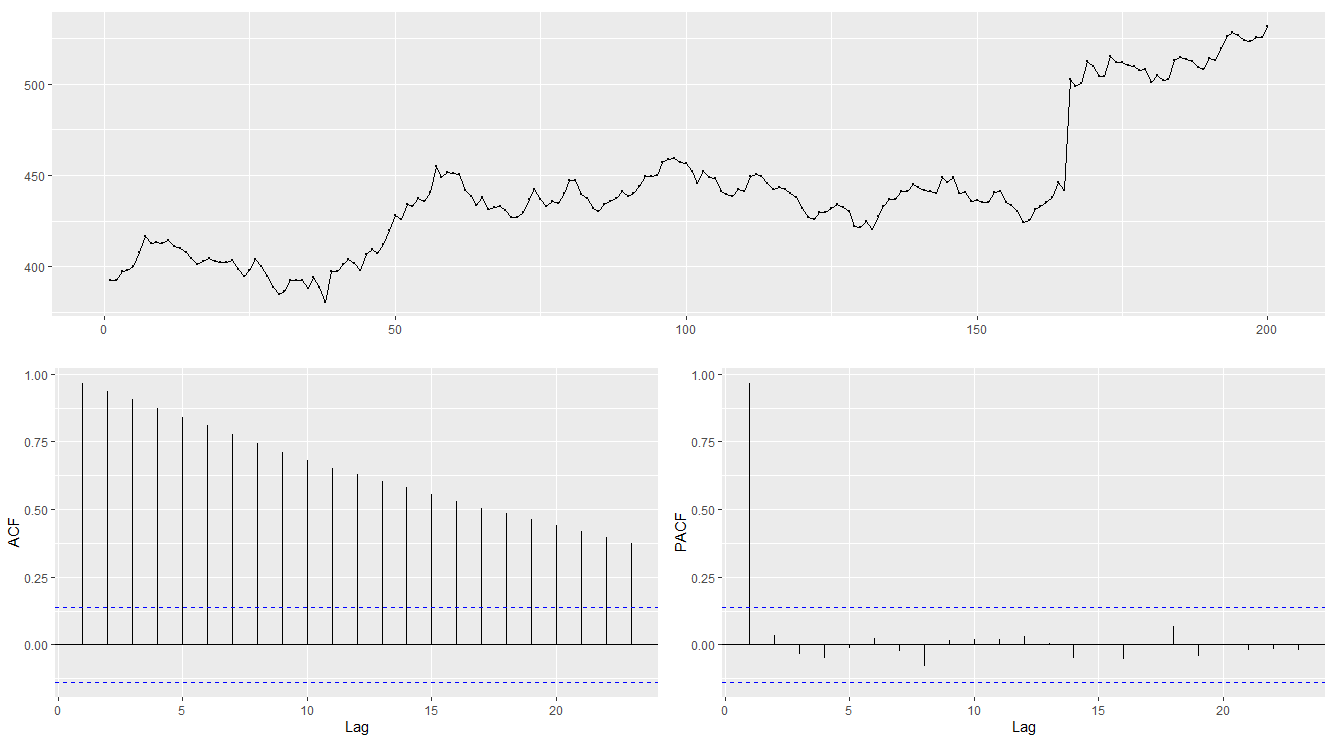
위의 그래프가 원본 데이터인데, 시간이 지나면서 계속 값이 증가하는 추세가 보이네요.
ACF 그래프를 봐도 시차가 커져도 계속 autocorrelation이 남아 있는 것을 볼 수 있습니다.
goog200 %>% adf.test() # p-value가 0.05보다 크다 = 귀무가설 채택(귀무가설 : 단위근이 있다)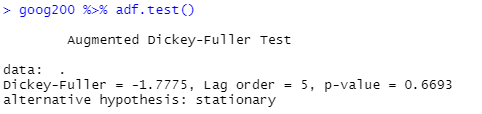
ADF 검정 결과, p-value가 0.05보다 커서 우리는 대립가설을 통계적으로 채택할 수 없게 됩니다. 즉, 해당 데이터는 단위근이 있고 Stationary하지 않다는 뜻이죠. 그러면 차분을 한 이후에도 단위근이 남아있는지 확인을 해 봅시다.
diff(goog200) %>% adf.test()
ggtsdisplay(diff(goog200))
차분을 하고 나니 단위근이 있다는 귀무가설을 더 이상 채택하지 못하게 됩니다! 대립가설인 stationary를 채택할 수 있게 됩니다.
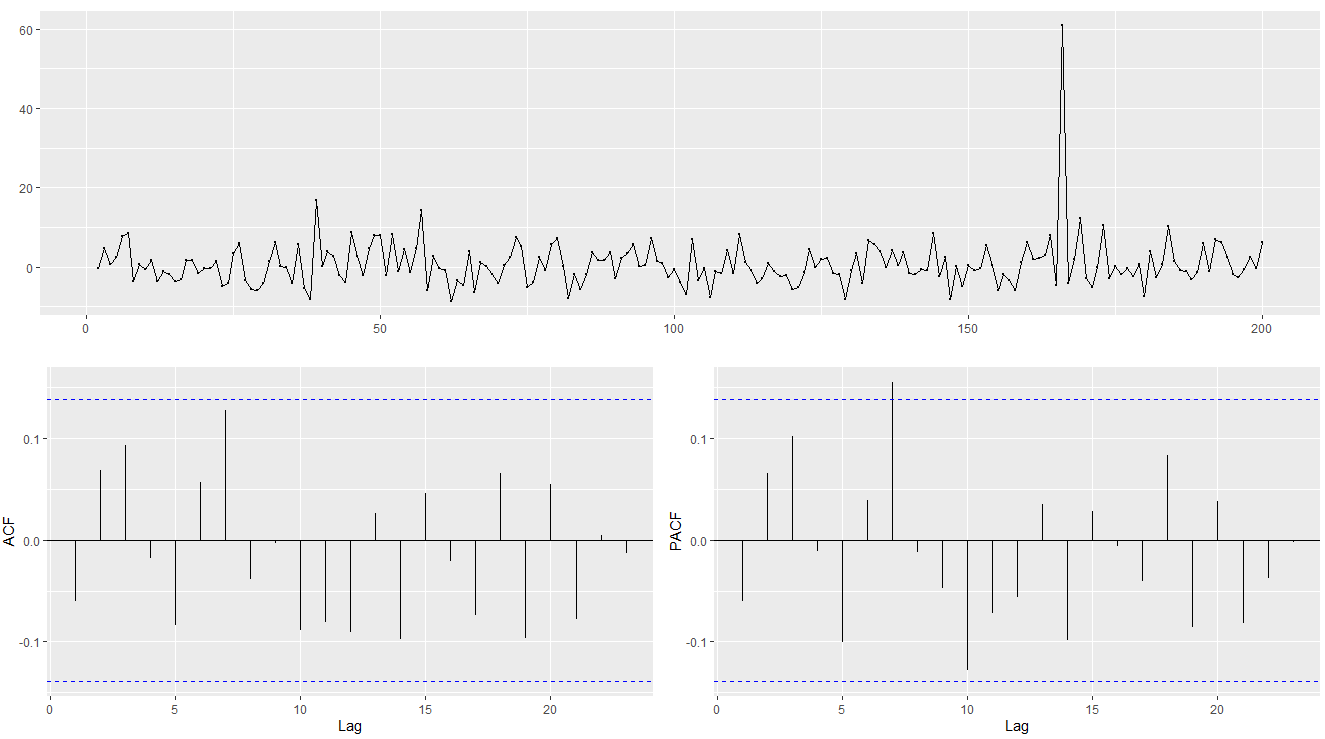
차분을 한 그래프를 보면 약간 다른 날에 비해 튀는 지점이 보이기는 하지만 ACF 그래프에서 데이터 간 autocorrelation이 대체로 0에 가까워진 것을 보아 데이터가 정상성에 가깝게 변화한 것을 볼 수 있습니다.
자기상관 검정
자기상관검정은 잔차 간 자기상관이 있는지를 확인하는 검정입니다. 만일 잔차에 자기상관이 있다면, 어제의 shock가 오늘의 shock에 영향을 미친다는 것입니다. 즉, 잔차(내가 예상못한 쇼크)는 백색잡음(White Noise)로 작용하여 시점끼리는 자기상관이 없어야 한다는 것입니다.
대표적인 검정으로는 Durbin-Watson 검정, Ljung-Box 검정 등이 있지만 저는 Ljung Box 검정에 대해서만 실습을 해보려고 합니다.
## 차분을 한 데이터로 auto.arima 시행
model <- diff(goog200) %>% auto.arima()
checkresiduals(model)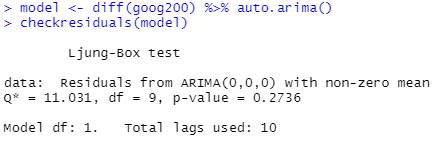
auto.arima로 적합한 ARIMA 모형을 찾고, checkresidual이라는 명령어를 통해 잔차의 상태를 진단해보았습니다.
auto.arima가 찾은 최적모형은 ARIMA(0,0,0) = 즉, 로데이터에서 차분만 한 데이터만으로도 충분히 모델링을 만족한다고 보았고, Ljung-Box test 결과 p-value가 0.2736으로 귀무가설 = 잔차 간 자기상관이 없다를 채택할 수 있게 되었습니다.
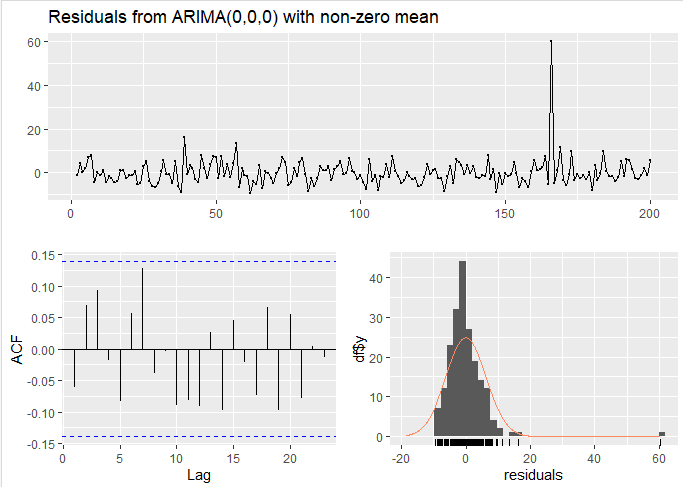
그림을 보아도 잔차의 ACF가 특별히 자기상관을 갖고 있는 거처럼 보이지는 않고(전부 파란 점선 안에 ACF가 들어와 있으므로), 잔차의 분포도 특정 이상치가 하나 있기는 하지만 전반적으로 크게 특이사항이 없는 것으로 보입니다.
요약
결과적으로 제가 헷갈렸던 건 정상성 = 백색잡음이라고 생각했던 부분이었습니다.
- 단위근 검정에서 바라보는 자기상관은 데이터 간 자기상관이 있어도 되지만 그게 시점이 아닌 시차에만 의존하면 되는 것이었습니다.
- 대신 Ljung-box test는 잔차의 자기상관이 있는지를 보는 검정이고, 잔차는 백색잡음이라고 가정을 했기 때문에 어떻게 보면 좀 더 단위근검정에서 바라보는 자기상관보다 빡빡한 기준을 적용하고 있던 것이었습니다.
- 그리고 단위근 검정은 본격적으로 데이터를 분석하기 전에 정상성을 만족시키기 위한 방법을 위한 검정이고,
- Ljung-Box test와 같은 자기상관검정은 분석이 완료된 이후에도 잔차(모델로 설명되지 않는 쇼크)에 자기상관이 남아있다면, 추가적으로 모델링을 더 진행해야 하므로, 현 시점의 모델링이 어느 정도로 정리가 되었는지 확인하기 위한 검정이라 목적성이 다르다는 차이가 있었습니다.
개인적으로는 이번에 헷갈리는 부분들을 정리하는 계기가 되어 좋았습니다..!
'Statistics' 카테고리의 다른 글
| 인과추론 학습기 - 00. 왜 인과추론인가? (공부이유, 학습자료) (0) | 2023.01.08 |
|---|---|
| ARIMA, SARIMA(계절성 ARIMA) 에 대하여 (2) | 2022.09.28 |
| 통계학에서 자주 활용되는 확률분포에 대해 (0) | 2022.08.19 |
| 주성분 분석(PCA)을 정리해보자! (0) | 2022.06.21 |
| 삶에 적용해 보는 인과분석 (0) | 2022.06.04 |
