시계열 공부를 하며 이래저래 인생에 적용해봄직한 부분을 정리해 보았습니다. 수식은 최소화하고 감성은 한껏 담아 글을 써보려고 합니다.
1. Wold Decomposition & Stationary(정상성)
'오늘의 나'라는 존재는 단독으로 존재할 수 없는 법입니다. 이게 무슨 해괴망측한 소리인가 하면, 어제의 나, 그제의 나, 일주일 전의 나, 몇 개월 전의 나라는 존재가 경험한 것들이 있었기에 "오늘의 내"가 존재할 수 있다는 것이지요. 그리고 내일의 나도 오늘의 나의 영향력에서 자유롭지 못할 것입니다.
$$Y_{T} =\mu + \psi_{t-1}e_{t-1} + \psi_{t-2}e_{t-2}+ \psi_{t-3}e_{t-3}+\psi_{t-4}e_{t-4}+... \psi_{t-j}e_{t-j} + ...$$
수식을 최소화하겠다고 써놓자마자, 수식을 쓰게 되어 머쓱하기는 하지만,
수식을 간단히 설명하면, 오늘의 나(Yt)라는 존재는 나라는 인간이 타고난 성질(mu)과 전일 내가 받았던 충격, 전전일 내가 받았던 충격 등등의 합으로 정의될 수 있다는 것입니다.
위와 같이 수식을 전개하는 것을 Wold Decomposition이라 합니다.
이제 Wold Decomposition 모형을 기반으로 조금 더 이야기를 진행해보려고 합니다.
'3X살의 나'의 감정은 '20살 대학 입시에 성공했던 10년 전'의 감정보다 '어제 당했던 거지같은 일들(?)'에 더 큰 영향을 받을 것입니다. 그리고 초등학교 때 느꼈던 소소한 행복, 고등학교 때 느꼈던 슬픔 등은 더더욱 영향력이 적을 것입니다. 이렇게 과거의 영향력은 갈수록 적어져야만 stationary(정상성) 조건을 만족할 수 있습니다.
그러니까 나라는 사람의 감정이 어느 정도 등락은 있지만 결국 어느 평균점에 회귀할 것이고, 그 등락도 편차가 어느 정도 일정할 것이라는 가정이죠. 만약 과거의 영향력이 작아지지 않고 현 시점까지 강하게 영향력을 미친다면, 나라는 사람의 감정은 과거의 경험으로 인한 것들이 계속 누적되어 stationary(정상성) 조건을 만족하지 못할 것입니다. 위 모형 기준으로는 j가 무한대에 가깝게 커지면, coefficient도 0에 수렴이 된다고 볼 수 있을 것입니다.
그러면 해당 모형을 알게 된다는 것은 어떤 의미일까요? 물론 나 자신이 신이 아니기에, 모형의 형태가 어떻게 될 지, 각 coefficient가 어떨지 알 수 없지만 만약 "나라는 인간"에 대한 모형을 정확히 알 수 있다면, 오늘 내가 받은 충격이 3일 후에 어느 정도로 영향을 미칠지, 혹은 N일 후에 어느 정도 영향을 미칠 지 알 수 있게 됩니다.
$$\frac{\partial Y_{t}}{\partial e_{t-3}} = \frac{\partial Y_{t+3}}{\partial e_{t}} = \psi_{3}$$
coefficient를 통해 바로 충격이 얼마나 효과가 지속될지를 예측할 수 있게 되지만, 데이터의 개수가 유한하다면 해당 모형은 parameter가 데이터의 개수보다 많아지게 됩니다. 이 경우 자유도가 음수가 되고, 사실상 예측이 불가능하게 된다는 결론에 부딪히게 되어 버립니다. 그럼 이렇게 길게 이야기한 것이 무용해지는 걸까요? 이 모형의 이점을 무용하게 만들지 않기 위해 보통 시계열에서 많이 이야기하는 ARMA 모형을 통해 approximation을 시키게 됩니다.
2. Random Walk
위에서 정상성은 장기적으로 평균으로 회귀하는 성질이라고 언급했습니다. 그러면 비정상성은 그 반대라고 볼 수 있겠죠. 시간이 지남에 따라 평균이 영향을 받거나, 평균은 일정하더라도 분산이 시간에 영향을 받으면, 그러니까 시간이 지남에 따라 평균으로 돌아오는 정도가 들쑥날쑥하다면 이는 비정상성을 가진다고 합니다.
이 중 비정상성을 갖는 것으로 가장 대표적인 모형이 랜덤워크입니다. 해당 모형은 위 아래로 확률적으로 이동하는 모습이 비틀비틀 걷는 취객의 걸음걸이와 유사하다는 비유로 언급되기도 합니다.
$$Y_{t} = Y_{t-1} + e_{t} + (\mu)$$
수식으로는 이렇게 쓰는데, 시간이 지남에 따라 평균으로 돌아갈 기미가 안 보이고, 다음 날의 예측값은 오늘의 상태와 오차항에 따라 랜덤으로 결정되게 됩니다. 심지어 상수항(drift)이 붙어있게 되면 시간이 지남에 따라 상수항은 누적되게 됩니다. 마치 트라우마가 남을 정도로 마음의 충격을 받게 되면, 이후에 작은 충격도 바로 회복하지 못하고 상처를 누적시키는 것과 비슷하다고 볼 수 있습니다. (엄밀히는 정확한 이야기는 아니지만 일종의 비유로요!)
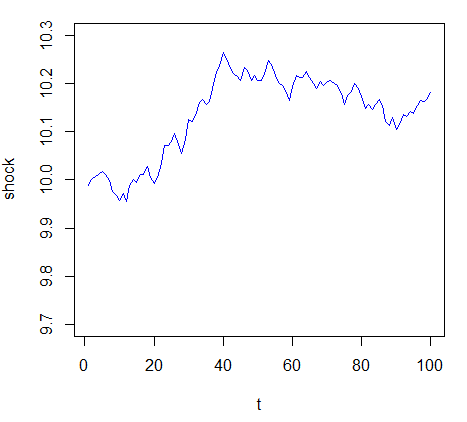
상수항이 붙어있지 않으면 랜덤워크 모형은 특별히 평균으로 회귀하려는 경향은 없이 당일 충격에 따라 값이 왔다갔다 하게 됩니다. 마음의 고향을 잃고 방황하는 것과 비슷하지요.
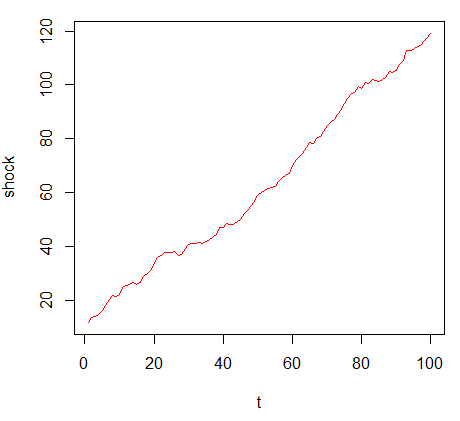
상수항이 붙어있는 모형은 t*mu만큼 값이 누적됩니다. 상수항은 평균으로 회귀하지 않고 영구적으로 충격을 남기게 됩니다.
3. ARCH 모형
돌이켜보면 그대로의 나인데, 슬럼프에 빠진 어느 순간에는 감정의 등락폭이 커지고, 마음의 회복이 더디게 느껴지는 순간이 있습니다. 그러니까 장기적으로는 감정의 등락폭이 일정하지만, 내가 슬럼프에 빠져 있다는 조건 하에서는 등락폭이 들쑥날쑥 달라지게 됩니다.
이러한 마음 상태에 ARCH(AutoRegressive Conditional Heteroskedasticity) 모형을 비유할 수 있을 것 같습니다.
ARCH 모형은 Engle이라는 경제학자가 발견한 모형으로, 어떤 기간동안에는 수익률의 변동성이 크게 지속되고 어떤 기간 동안에는 변동성이 작게 지속되는 것을 발견하고 이를 모형화한 것이라고 합니다. 조건부로는 이분산을 갖지만, Unconditional할 때, 그러니까 장기적으로는 등분산을 갖는 모형입니다.
내 마음을 ARCH 모형에 비유하면, 지금이 슬럼프라고 마음이 오락가락 하더라도, 장기적으로는 돌아올 수 있다는 희망을 가질 수 있을 것입니다.
오르락 내리락을 왔다갔다 하더라도, "나"라는 사람이 정상성을 갖는다면, 결국 평균으로 회귀할 수 있을 것입니다. 그러면 왔다갔다 하면서 내가 어느 상태로 수렴하는지에 대한 정보를 파악할 수 있을 것이고, 그러면 마음이 들썩거리는 과정을 통해 "나"라는 사람의 본질을 알아갈 수 있을 것입니다.
때로는 하루 하루 살아가는 것이 쉽지 않지만, 나라는 사람을 fine tuning 하는 과정이라 생각하며 어려움을 잘 극복해나가면 좋겠다는 메시지로, 급하게 훈훈하게 마무리 해봅니다.
'Statistics' 카테고리의 다른 글
| 삶에 적용해 보는 인과분석 (0) | 2022.06.04 |
|---|---|
| 기초 선형대수학 개념 정리 (feat.회귀분석) (0) | 2022.05.26 |
| 수리통계학 - EM 알고리즘 (0) | 2021.09.17 |
| 수리통계학 - MLE와 MVUE에 대하여 (2) | 2021.08.28 |
| 수리통계학 - 추정량을 선택하는 기준에 대하여 (0) | 2021.08.10 |
시계열 공부를 하며 이래저래 인생에 적용해봄직한 부분을 정리해 보았습니다. 수식은 최소화하고 감성은 한껏 담아 글을 써보려고 합니다.
1. Wold Decomposition & Stationary(정상성)
'오늘의 나'라는 존재는 단독으로 존재할 수 없는 법입니다. 이게 무슨 해괴망측한 소리인가 하면, 어제의 나, 그제의 나, 일주일 전의 나, 몇 개월 전의 나라는 존재가 경험한 것들이 있었기에 "오늘의 내"가 존재할 수 있다는 것이지요. 그리고 내일의 나도 오늘의 나의 영향력에서 자유롭지 못할 것입니다.
$$Y_{T} =\mu + \psi_{t-1}e_{t-1} + \psi_{t-2}e_{t-2}+ \psi_{t-3}e_{t-3}+\psi_{t-4}e_{t-4}+... \psi_{t-j}e_{t-j} + ...$$
수식을 최소화하겠다고 써놓자마자, 수식을 쓰게 되어 머쓱하기는 하지만,
수식을 간단히 설명하면, 오늘의 나(Yt)라는 존재는 나라는 인간이 타고난 성질(mu)과 전일 내가 받았던 충격, 전전일 내가 받았던 충격 등등의 합으로 정의될 수 있다는 것입니다.
위와 같이 수식을 전개하는 것을 Wold Decomposition이라 합니다.
이제 Wold Decomposition 모형을 기반으로 조금 더 이야기를 진행해보려고 합니다.
'3X살의 나'의 감정은 '20살 대학 입시에 성공했던 10년 전'의 감정보다 '어제 당했던 거지같은 일들(?)'에 더 큰 영향을 받을 것입니다. 그리고 초등학교 때 느꼈던 소소한 행복, 고등학교 때 느꼈던 슬픔 등은 더더욱 영향력이 적을 것입니다. 이렇게 과거의 영향력은 갈수록 적어져야만 stationary(정상성) 조건을 만족할 수 있습니다.
그러니까 나라는 사람의 감정이 어느 정도 등락은 있지만 결국 어느 평균점에 회귀할 것이고, 그 등락도 편차가 어느 정도 일정할 것이라는 가정이죠. 만약 과거의 영향력이 작아지지 않고 현 시점까지 강하게 영향력을 미친다면, 나라는 사람의 감정은 과거의 경험으로 인한 것들이 계속 누적되어 stationary(정상성) 조건을 만족하지 못할 것입니다. 위 모형 기준으로는 j가 무한대에 가깝게 커지면, coefficient도 0에 수렴이 된다고 볼 수 있을 것입니다.
그러면 해당 모형을 알게 된다는 것은 어떤 의미일까요? 물론 나 자신이 신이 아니기에, 모형의 형태가 어떻게 될 지, 각 coefficient가 어떨지 알 수 없지만 만약 "나라는 인간"에 대한 모형을 정확히 알 수 있다면, 오늘 내가 받은 충격이 3일 후에 어느 정도로 영향을 미칠지, 혹은 N일 후에 어느 정도 영향을 미칠 지 알 수 있게 됩니다.
$$\frac{\partial Y_{t}}{\partial e_{t-3}} = \frac{\partial Y_{t+3}}{\partial e_{t}} = \psi_{3}$$
coefficient를 통해 바로 충격이 얼마나 효과가 지속될지를 예측할 수 있게 되지만, 데이터의 개수가 유한하다면 해당 모형은 parameter가 데이터의 개수보다 많아지게 됩니다. 이 경우 자유도가 음수가 되고, 사실상 예측이 불가능하게 된다는 결론에 부딪히게 되어 버립니다. 그럼 이렇게 길게 이야기한 것이 무용해지는 걸까요? 이 모형의 이점을 무용하게 만들지 않기 위해 보통 시계열에서 많이 이야기하는 ARMA 모형을 통해 approximation을 시키게 됩니다.
2. Random Walk
위에서 정상성은 장기적으로 평균으로 회귀하는 성질이라고 언급했습니다. 그러면 비정상성은 그 반대라고 볼 수 있겠죠. 시간이 지남에 따라 평균이 영향을 받거나, 평균은 일정하더라도 분산이 시간에 영향을 받으면, 그러니까 시간이 지남에 따라 평균으로 돌아오는 정도가 들쑥날쑥하다면 이는 비정상성을 가진다고 합니다.
이 중 비정상성을 갖는 것으로 가장 대표적인 모형이 랜덤워크입니다. 해당 모형은 위 아래로 확률적으로 이동하는 모습이 비틀비틀 걷는 취객의 걸음걸이와 유사하다는 비유로 언급되기도 합니다.
$$Y_{t} = Y_{t-1} + e_{t} + (\mu)$$
수식으로는 이렇게 쓰는데, 시간이 지남에 따라 평균으로 돌아갈 기미가 안 보이고, 다음 날의 예측값은 오늘의 상태와 오차항에 따라 랜덤으로 결정되게 됩니다. 심지어 상수항(drift)이 붙어있게 되면 시간이 지남에 따라 상수항은 누적되게 됩니다. 마치 트라우마가 남을 정도로 마음의 충격을 받게 되면, 이후에 작은 충격도 바로 회복하지 못하고 상처를 누적시키는 것과 비슷하다고 볼 수 있습니다. (엄밀히는 정확한 이야기는 아니지만 일종의 비유로요!)

상수항이 붙어있지 않으면 랜덤워크 모형은 특별히 평균으로 회귀하려는 경향은 없이 당일 충격에 따라 값이 왔다갔다 하게 됩니다. 마음의 고향을 잃고 방황하는 것과 비슷하지요.

상수항이 붙어있는 모형은 t*mu만큼 값이 누적됩니다. 상수항은 평균으로 회귀하지 않고 영구적으로 충격을 남기게 됩니다.
3. ARCH 모형
돌이켜보면 그대로의 나인데, 슬럼프에 빠진 어느 순간에는 감정의 등락폭이 커지고, 마음의 회복이 더디게 느껴지는 순간이 있습니다. 그러니까 장기적으로는 감정의 등락폭이 일정하지만, 내가 슬럼프에 빠져 있다는 조건 하에서는 등락폭이 들쑥날쑥 달라지게 됩니다.
이러한 마음 상태에 ARCH(AutoRegressive Conditional Heteroskedasticity) 모형을 비유할 수 있을 것 같습니다.
ARCH 모형은 Engle이라는 경제학자가 발견한 모형으로, 어떤 기간동안에는 수익률의 변동성이 크게 지속되고 어떤 기간 동안에는 변동성이 작게 지속되는 것을 발견하고 이를 모형화한 것이라고 합니다. 조건부로는 이분산을 갖지만, Unconditional할 때, 그러니까 장기적으로는 등분산을 갖는 모형입니다.
내 마음을 ARCH 모형에 비유하면, 지금이 슬럼프라고 마음이 오락가락 하더라도, 장기적으로는 돌아올 수 있다는 희망을 가질 수 있을 것입니다.
오르락 내리락을 왔다갔다 하더라도, "나"라는 사람이 정상성을 갖는다면, 결국 평균으로 회귀할 수 있을 것입니다. 그러면 왔다갔다 하면서 내가 어느 상태로 수렴하는지에 대한 정보를 파악할 수 있을 것이고, 그러면 마음이 들썩거리는 과정을 통해 "나"라는 사람의 본질을 알아갈 수 있을 것입니다.
때로는 하루 하루 살아가는 것이 쉽지 않지만, 나라는 사람을 fine tuning 하는 과정이라 생각하며 어려움을 잘 극복해나가면 좋겠다는 메시지로, 급하게 훈훈하게 마무리 해봅니다.
'Statistics' 카테고리의 다른 글
| 삶에 적용해 보는 인과분석 (0) | 2022.06.04 |
|---|---|
| 기초 선형대수학 개념 정리 (feat.회귀분석) (0) | 2022.05.26 |
| 수리통계학 - EM 알고리즘 (0) | 2021.09.17 |
| 수리통계학 - MLE와 MVUE에 대하여 (2) | 2021.08.28 |
| 수리통계학 - 추정량을 선택하는 기준에 대하여 (0) | 2021.08.10 |
