지난번 작성했던 글에 이어 오늘도 수리통계학, 그 중에서도 MLE(maximum likelihood estimation)에 대해 작성해보려고 한다.
https://blessedby-clt.tistory.com/23
수리통계학 - 추정량을 선택하는 기준에 대하여
누군가 통계학이란 어떤 학문이냐고 묻는다면, 나는 "미지의 모수를 추정하는 학문"이라고 답할 것이다. '추정'이라는 것은 정확하지는 않지만 어슴프레하게나마 어떤 값을 맞춰보겠다는 것이
blessedby-clt.tistory.com
MLE란 무엇인가
지난번 작성했던 글에서,
- likelihood는 X1, ..., Xn이 발생했고, 발생한 사실로 비추어볼때 어떤 모수가 도출될 가능성(likelihood)에 대한 것이다.
라고 간략하게 언급했는데, 조금은 구체적이지만 말도 안 되는 예시를 들면 다음과 같다.
비 vs 맑음 둘 중 하나만 존재하고, 기후라고 할 것도 없어서 날씨가 랜덤으로 정해지는 세계가 있다고 가정하자.(날씨조차 흑백논리로 가득한 세계는 이 세상 어디에도 없겠지만서도)
그러면 100일 동안의 날씨 기록으로 '비'가 올 확률을 추정해보려고 한다.
이 케이스면 모 아니면 도... 아니 0 아니면 1이므로 베르누이 분포를 따르게 될 것이다.
먼저 베르누이 분포 하에서 likelihood를 구하는 함수를 정의해본다. X1, ..., Xn의 joint pdf를 사용해서 모수인 theta를 예측해보려고 하는 것이다.
likelihood.Bernoulli = function(theta, x) {
# theta success probability parameter
# x vector of data
n = length(x) ## 시행횟수
ans = theta^sum(x) * (1-theta)^(n-sum(x))
## joint pdf. 단 theta로 표현되는 모수가 변동, 관측 결과는 변하지 않는다.
return(ans)
}
일단 비가 올 확률은 25%라고 세팅해두었다. 물론 확률은 25%여도 실제 관측값이 25%로 나온다는 보장은 없다. 확률은 어디까지나 확률일 뿐이니까... 아무튼 25%라는 확률이 가정되었지만 이를 모르는 상태에서 100일동안 날씨를 관측한 결과값을 갖고 있다.
이 때 관측한 결과값은 그대로 유지한 채, 0%, 1%, 2%... 각각의 확률을 변수로 likelihood 함수에 넣었을 때 likelihood를 가장 크게 만드는 확률, 그것을 MLE로 정하려고 한다.
x = rbinom(100, 1, 0.25)
theta.vals = seq(0,1, length.out=101)
## 0% 부터 100%까지의 확률값 모음.
like.vals = likelihood.Bernoulli(theta.vals, x)
## 위에서 만든 likelihood를 구하는 함수.
## 결과적으로 확률값 모음을 각각 하나씩 넣어봤을 때 likelihood가 제일 큰 것을 MLE로 채택.
data <- as.data.frame(cbind(theta.vals, like.vals))
ggplot(data = data, aes(x = theta.vals, y = like.vals)) + geom_point(colour = "blue")
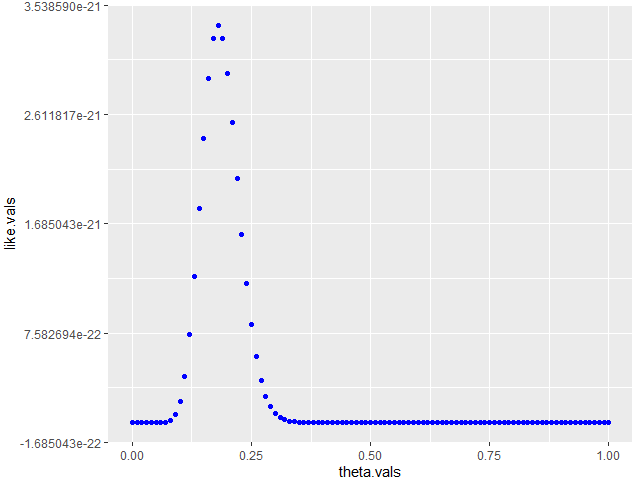
그렇게 구한 likelihood plot이다. 18%의 확률로 가정하는 것이 likelihood가 가장 크게 나와서, 이 경우 18%를 채택하게 될 것이다. 25%랑은 살짝 차이가 있는 값이지만, 제한된 정보 하에서 추정한 값 치고는 합리적이라고 볼 수도 있다.
MLE가 좋은 통계량이라는 것에 대해서는
- 일치성(consistency)을 만족하고,
- 위에서 언급한 CLT와 유사하게 근사적으로 Normal distribution으로 수렴하는 특징
이 있기 때문이라고 언급했었는데, 하나 더 좋은 이유를 추가해서 설명하려고 한다.
그것은 MVUE(minimum variance unbiased estimator)를 구함에 있어 MLE가 좋은 시작점이 될 수 있다는 것이다.
새로운 용어가 등장했다. MVUE가 뭔데 이 녀석아 라고 할 수도 있겠지만, minimum variance unbiased estimator, 즉 불편추정량 중에서 분산이 가장 작은 추정량을 의미한다. 어떻게 보면 추정량이 갖추어야 할 미덕을 두루 갖춘 팔방미인 추정량이라고 볼 수 있는데, 그렇다면 어떻게 MLE가 MVUE를 구함에 있어 좋은 시작점이 될 수 있다는 것일까?
충분통계량이란?
이를 위해서는 충분통계량(sufficiency statistic)을 언급해야 한다. 도대체 무엇이 충분한걸까.. 라는 의문이 드는데, 충분통계량의 정의를 보면 대략적으로 추측이 된다.
$$ X_{1},...,X_{n} \sim iid \: \: f(x;\Theta ) $$
$$ Y_{1} = u(X_{1}, ..., X_{n}) \sim f(y;\Theta ) $$
$$ \frac{f(x_{1};\Theta)*f(x_{2};\Theta)*...*f(x_{n};\Theta)}{f_{Y_{1}}[u(X_{1}, ..., X_{n});\Theta ]} = H(x_{1},...,x_{n}) $$
일 때 Y1은 충분통계량이라는 것이다.
아니 이게 도대체 뭔 소리야, 싶겠지만... X1,...,Xn의 joint pdf은 Y1이라는 통계량과 theta(모수)와는 관계없는 수식으로 분리가 된다는 것이고, 그 말인즉슨 Y1라는 통계량 하나만으로 "충분히" 모수에 대한 정보를 포함하고 있다는 뜻이다.
X1, ..., Xn 다 고려할 필요 없이 Y1만 있으면 모수에 대한 정보를 추정할 수 있다는 것과 MVUE는 무슨 연관관계가 있을까?
그것은 충분통계량과 관련한 Theroem, Rao-Blackwell Theorem과 관계가 있다.
Rao-Blackwell Theorem
$$ X_{1},...,X_{n} \sim iid \: \: f(x;\Theta ) $$
Y1은 X1,...,Xn으로 이루어진 함수이자 충분통계량이고,
Y2는 X1, ..., Xn으로 이루어진 함수이고, 불편통계량이라고 가정할 때(대신 Y1의 함수는 아니어야 한다.)
$$ E[Y_{2}|Y_{1}] = \Psi(Y_{1}) $$
이라는 함수를 만들 수 있고, 이 경우 아래와 같은 성질을 갖게 된다.
$$ E[\Psi(Y_{1})] = \Theta \; \; and \; \; Var[\Psi(Y_{1})] < Var(Y_{2}) $$
이 역시 링크로 대체하고, 자세한 증명은 생략한다.
Y2|Y1인 조건부 분포도 불편 추정량이고, 최초의 불편추정량이었던 Y2보다도 분산이 작게 나온다는 것이다. 최소불편추정량의 단초가 충분통계량에서 나온다.
그리고 또 다른 Theorem이 하나 더 있다.
MLE가 uniqe한 경우에는 mle도 Y1의 함수가 될 수 있다는 것인데, 즉, 위에서 언급한 Rao-blackwell Theorem을 적용할 수 있어서 MLE는 꽤나 좋은 통계량이 될 수 있다.
물론 Rao-Blackwell Theorem 만으로는 최소불편추정량이라고 말할 수 없다. 현재까지는 상대적으로 분산이 작은 추정량만 말했으니까...
하지만 완비통계량(Completeness statistic)이라는 조건과, Lehmann and Scheffe Theorem을 적용하면 MVUE를 증명할 수는 있는데, 여기까지 가면 수식이 더 길고 복잡해지므로 거기까지는 이 포스팅에서 언급하지 않으려고 한다....
다만,
- MLE는 충분통계량의 함수가 될 수 있고,
- MLE를 활용해서 불편추정량을 만들어낼 수 있으면
- 이것은 일단 MVUE의 좋은 후보가 될 수 있다!
는 것으로 해당 포스팅을 결론짓고 마무리한다.
총총.
참고 링크
likelihood function 작성 코드 : https://faculty.washington.edu/ezivot/econ424/maximumLikelihood.r
충분통계량 : https://syj9700.tistory.com/4
'Statistics' 카테고리의 다른 글
| 감성 시계열 - 정상성, Random-Walk, ARCH에 대한 감성적 견해 (0) | 2021.12.18 |
|---|---|
| 수리통계학 - EM 알고리즘 (0) | 2021.09.17 |
| 수리통계학 - 추정량을 선택하는 기준에 대하여 (0) | 2021.08.10 |
| 시계열 분석 - ARIMA 모형 정리 (0) | 2021.04.17 |
| 헷갈리는 회귀분석의 기록(2) - 회귀분석 모형 진단 (0) | 2021.02.07 |
지난번 작성했던 글에 이어 오늘도 수리통계학, 그 중에서도 MLE(maximum likelihood estimation)에 대해 작성해보려고 한다.
https://blessedby-clt.tistory.com/23
수리통계학 - 추정량을 선택하는 기준에 대하여
누군가 통계학이란 어떤 학문이냐고 묻는다면, 나는 "미지의 모수를 추정하는 학문"이라고 답할 것이다. '추정'이라는 것은 정확하지는 않지만 어슴프레하게나마 어떤 값을 맞춰보겠다는 것이
blessedby-clt.tistory.com
MLE란 무엇인가
지난번 작성했던 글에서,
- likelihood는 X1, ..., Xn이 발생했고, 발생한 사실로 비추어볼때 어떤 모수가 도출될 가능성(likelihood)에 대한 것이다.
라고 간략하게 언급했는데, 조금은 구체적이지만 말도 안 되는 예시를 들면 다음과 같다.
비 vs 맑음 둘 중 하나만 존재하고, 기후라고 할 것도 없어서 날씨가 랜덤으로 정해지는 세계가 있다고 가정하자.(날씨조차 흑백논리로 가득한 세계는 이 세상 어디에도 없겠지만서도)
그러면 100일 동안의 날씨 기록으로 '비'가 올 확률을 추정해보려고 한다.
이 케이스면 모 아니면 도... 아니 0 아니면 1이므로 베르누이 분포를 따르게 될 것이다.
먼저 베르누이 분포 하에서 likelihood를 구하는 함수를 정의해본다. X1, ..., Xn의 joint pdf를 사용해서 모수인 theta를 예측해보려고 하는 것이다.
likelihood.Bernoulli = function(theta, x) {
# theta success probability parameter
# x vector of data
n = length(x) ## 시행횟수
ans = theta^sum(x) * (1-theta)^(n-sum(x))
## joint pdf. 단 theta로 표현되는 모수가 변동, 관측 결과는 변하지 않는다.
return(ans)
}
일단 비가 올 확률은 25%라고 세팅해두었다. 물론 확률은 25%여도 실제 관측값이 25%로 나온다는 보장은 없다. 확률은 어디까지나 확률일 뿐이니까... 아무튼 25%라는 확률이 가정되었지만 이를 모르는 상태에서 100일동안 날씨를 관측한 결과값을 갖고 있다.
이 때 관측한 결과값은 그대로 유지한 채, 0%, 1%, 2%... 각각의 확률을 변수로 likelihood 함수에 넣었을 때 likelihood를 가장 크게 만드는 확률, 그것을 MLE로 정하려고 한다.
x = rbinom(100, 1, 0.25)
theta.vals = seq(0,1, length.out=101)
## 0% 부터 100%까지의 확률값 모음.
like.vals = likelihood.Bernoulli(theta.vals, x)
## 위에서 만든 likelihood를 구하는 함수.
## 결과적으로 확률값 모음을 각각 하나씩 넣어봤을 때 likelihood가 제일 큰 것을 MLE로 채택.
data <- as.data.frame(cbind(theta.vals, like.vals))
ggplot(data = data, aes(x = theta.vals, y = like.vals)) + geom_point(colour = "blue")

그렇게 구한 likelihood plot이다. 18%의 확률로 가정하는 것이 likelihood가 가장 크게 나와서, 이 경우 18%를 채택하게 될 것이다. 25%랑은 살짝 차이가 있는 값이지만, 제한된 정보 하에서 추정한 값 치고는 합리적이라고 볼 수도 있다.
MLE가 좋은 통계량이라는 것에 대해서는
- 일치성(consistency)을 만족하고,
- 위에서 언급한 CLT와 유사하게 근사적으로 Normal distribution으로 수렴하는 특징
이 있기 때문이라고 언급했었는데, 하나 더 좋은 이유를 추가해서 설명하려고 한다.
그것은 MVUE(minimum variance unbiased estimator)를 구함에 있어 MLE가 좋은 시작점이 될 수 있다는 것이다.
새로운 용어가 등장했다. MVUE가 뭔데 이 녀석아 라고 할 수도 있겠지만, minimum variance unbiased estimator, 즉 불편추정량 중에서 분산이 가장 작은 추정량을 의미한다. 어떻게 보면 추정량이 갖추어야 할 미덕을 두루 갖춘 팔방미인 추정량이라고 볼 수 있는데, 그렇다면 어떻게 MLE가 MVUE를 구함에 있어 좋은 시작점이 될 수 있다는 것일까?
충분통계량이란?
이를 위해서는 충분통계량(sufficiency statistic)을 언급해야 한다. 도대체 무엇이 충분한걸까.. 라는 의문이 드는데, 충분통계량의 정의를 보면 대략적으로 추측이 된다.
$$ X_{1},...,X_{n} \sim iid \: \: f(x;\Theta ) $$
$$ Y_{1} = u(X_{1}, ..., X_{n}) \sim f(y;\Theta ) $$
$$ \frac{f(x_{1};\Theta)*f(x_{2};\Theta)*...*f(x_{n};\Theta)}{f_{Y_{1}}[u(X_{1}, ..., X_{n});\Theta ]} = H(x_{1},...,x_{n}) $$
일 때 Y1은 충분통계량이라는 것이다.
아니 이게 도대체 뭔 소리야, 싶겠지만... X1,...,Xn의 joint pdf은 Y1이라는 통계량과 theta(모수)와는 관계없는 수식으로 분리가 된다는 것이고, 그 말인즉슨 Y1라는 통계량 하나만으로 "충분히" 모수에 대한 정보를 포함하고 있다는 뜻이다.
X1, ..., Xn 다 고려할 필요 없이 Y1만 있으면 모수에 대한 정보를 추정할 수 있다는 것과 MVUE는 무슨 연관관계가 있을까?
그것은 충분통계량과 관련한 Theroem, Rao-Blackwell Theorem과 관계가 있다.
Rao-Blackwell Theorem
$$ X_{1},...,X_{n} \sim iid \: \: f(x;\Theta ) $$
Y1은 X1,...,Xn으로 이루어진 함수이자 충분통계량이고,
Y2는 X1, ..., Xn으로 이루어진 함수이고, 불편통계량이라고 가정할 때(대신 Y1의 함수는 아니어야 한다.)
$$ E[Y_{2}|Y_{1}] = \Psi(Y_{1}) $$
이라는 함수를 만들 수 있고, 이 경우 아래와 같은 성질을 갖게 된다.
$$ E[\Psi(Y_{1})] = \Theta \; \; and \; \; Var[\Psi(Y_{1})] < Var(Y_{2}) $$
이 역시 링크로 대체하고, 자세한 증명은 생략한다.
Y2|Y1인 조건부 분포도 불편 추정량이고, 최초의 불편추정량이었던 Y2보다도 분산이 작게 나온다는 것이다. 최소불편추정량의 단초가 충분통계량에서 나온다.
그리고 또 다른 Theorem이 하나 더 있다.
MLE가 uniqe한 경우에는 mle도 Y1의 함수가 될 수 있다는 것인데, 즉, 위에서 언급한 Rao-blackwell Theorem을 적용할 수 있어서 MLE는 꽤나 좋은 통계량이 될 수 있다.
물론 Rao-Blackwell Theorem 만으로는 최소불편추정량이라고 말할 수 없다. 현재까지는 상대적으로 분산이 작은 추정량만 말했으니까...
하지만 완비통계량(Completeness statistic)이라는 조건과, Lehmann and Scheffe Theorem을 적용하면 MVUE를 증명할 수는 있는데, 여기까지 가면 수식이 더 길고 복잡해지므로 거기까지는 이 포스팅에서 언급하지 않으려고 한다....
다만,
- MLE는 충분통계량의 함수가 될 수 있고,
- MLE를 활용해서 불편추정량을 만들어낼 수 있으면
- 이것은 일단 MVUE의 좋은 후보가 될 수 있다!
는 것으로 해당 포스팅을 결론짓고 마무리한다.
총총.
참고 링크
likelihood function 작성 코드 : https://faculty.washington.edu/ezivot/econ424/maximumLikelihood.r
충분통계량 : https://syj9700.tistory.com/4
'Statistics' 카테고리의 다른 글
| 감성 시계열 - 정상성, Random-Walk, ARCH에 대한 감성적 견해 (0) | 2021.12.18 |
|---|---|
| 수리통계학 - EM 알고리즘 (0) | 2021.09.17 |
| 수리통계학 - 추정량을 선택하는 기준에 대하여 (0) | 2021.08.10 |
| 시계열 분석 - ARIMA 모형 정리 (0) | 2021.04.17 |
| 헷갈리는 회귀분석의 기록(2) - 회귀분석 모형 진단 (0) | 2021.02.07 |
