오늘은 인과추론의 주요 개념 중 하나인 인과 그래프에 대한 글을 써보려고 한다.
- 독립, 조건부 독립 등 기초 통계
- 회귀분석에 대한 개념을 미리 알고 있어야 글을 이해하기 편할 것 같다.
글에서는 다루지는 않지만, 베이지안 통계에 대한 이해도가 있으면 아래 설명을 기반으로 심화된 내용을 확장해서 찾아보기 편할 것 같다.
기본 용어
SCM (Structural Causal Model)
한글로 그대로 직역하면 구조화된 인과모형이다. 즉, 인과관계를 구조적으로 설명하는 모델로서, 좀 더 자세히 말하면 변수 간의 인과 관계를 명시적으로 수식화하여 표현하는 모델이다. 이러한 모형을 사용하면 인과 관계의 방향성과 크기를 명확히 이해할 수 있다.
예를 들어 하루 섭취한 칼로리가 500kcal를 넘어갈 때마다 체중 1kg가 증가한다고 가정해 보자.(슬픈 가정이지만..)
그러면 증가한 체중(\(Y\)) := 500 * 초과 섭취한 칼로리(\(X\))라는 수식을 쓸 수 있다.
인과관계를 이렇게 수식으로 표현하는 것을 SCM이라고 한다.
외생변수, 내생변수
위의 관계 Y = 500*X라는 수식에서 체중(Y) 변수는 내생변수이다. 내생변수는 인과 모형 안에서 다른 변수에 의해 영향을 받는 변수, 즉, 인과 관계를 설명하는 데 사용되는 변수라는 의미이다. 칼로리 초과 섭취에 의해 체중의 변동이 일어나기 때문에 체중은 내생변수가 된다.
반면, 인과 모형 밖에서 결정되는 변수도 있다. 이를 외생변수라고 한다. 예를 들어 가을이 되면서 식욕이 늘어 섭취 칼로리가 늘었다고 해보자. 가을이라는 "계절"은 섭취 칼로리에 영향을 줄 수 있지만, 인과 모형(섭취칼로리와 체중이라는 인과모형) 밖에서 이미 결정된 변수이기 때문에 이를 외생변수라 부를 수 있게 된다.
잠깐 딴 소리를 하자면 위에서 말하는 외생변수, 내생변수는 회귀분석에서 말하는 내생성(endogeneity) 문제와 조금 결이 다르다. 회귀분석에서 말하는 내생성은 설명변수(독립변수)와 잔차 간에 상관성이 생기는 현상을 의미한다. 주로 누락된 변수(omitted variable problem 이라고도 한다.)나 잘못된 변수를 넣을 때 발생할 수 있다.
즉, 잔차항과 상관관계를 갖는 변수를 내생변수라고 하고, 그렇지 않은 변수를 외생변수라고 한다. (조금 딴 소리지만 외생변수에 대한 정의가 인과 그래프와 회귀분석에 조금 차이가 있어 첨언해 보았다.)
주요 그래프 용어
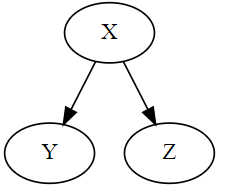
위에서 설명한 SCM을 기반으로 인과 그래프를 그릴 수 있다. 인과 그래프라고 하면 거창해 보이는데,
- 영향을 받는 변수를 화살표를 받는 쪽으로,
- 영향을 주는 변수를 화살표를 주는 쪽으로 놓고 그래프를 그리면 그게 인과 그래프다.
그리고 영향을 주고받는 각 변수를 노드(Node)로, 변수 간 관계를 엣지(Edge)라고 부른다.
그리고 보통 인과관계를 표현할 때 사용하는 그래프는 DAG (Directed Acyclic Graph) 형태를 지닌다. DAG라고 하니 이것도 마찬가지로 굉장히 거창해 보이지만, 직독직해하자면
- Directed : 방향성이 있고 (화살표가 포함되는 그래프)
- Acyclic : 순환하지 않는
- Graph : 그래프
라는 의미이다.
즉, X가 Y에 영향을 준다는 관계성을 표현해야 하기 때문에 화살표(방향성)가 필요하다. 또한, X가 Y에 영향을 주면서 Y가 X에 주는 순환관계(인과관계 - 역 인과관계 동시 성립)는 발생하지 않아야 한다.
인과 그래프가 중요한 이유
여기까지 신나게 SCM과 인과그래프에 대해 이야기했다. 인과 그래프가 회귀분석, 머신러닝 같은 분석에 사용되는 기법은 아니기 때문에 멋이 없어 보일 수도 있다. (사실 내가 처음 공부할 때 그랬음)
그런데 인과 그래프를 그려보는 것은 분석 기법을 적용하기 전에 거의 무조건 선행되어야 한다! 그렇지 않으면 소위 Bad Control 문제가 나타날 수 있기 때문이다.
회귀분석에 대해 배울 때 설명변수를 가려 넣으세요 와 같은 이야기를 들은 적이 있을까? 아마 다중공선성 문제가 없거나 과적합 문제가 없다는 가정 하에서 다양한 설명변수를 많이 넣고 보는 게 좋다고 배웠을 가능성이 클 것 같다. 예측문제에서는 쓸 수 있는 변수가 많은 것이 선(善)이라고 볼 수 있지만, 인과 관계를 추론할 때는 아무 변수나 막 넣으면 오히려 인과관계를 왜곡하여 해석할 수 있는 여지가 발생한다.
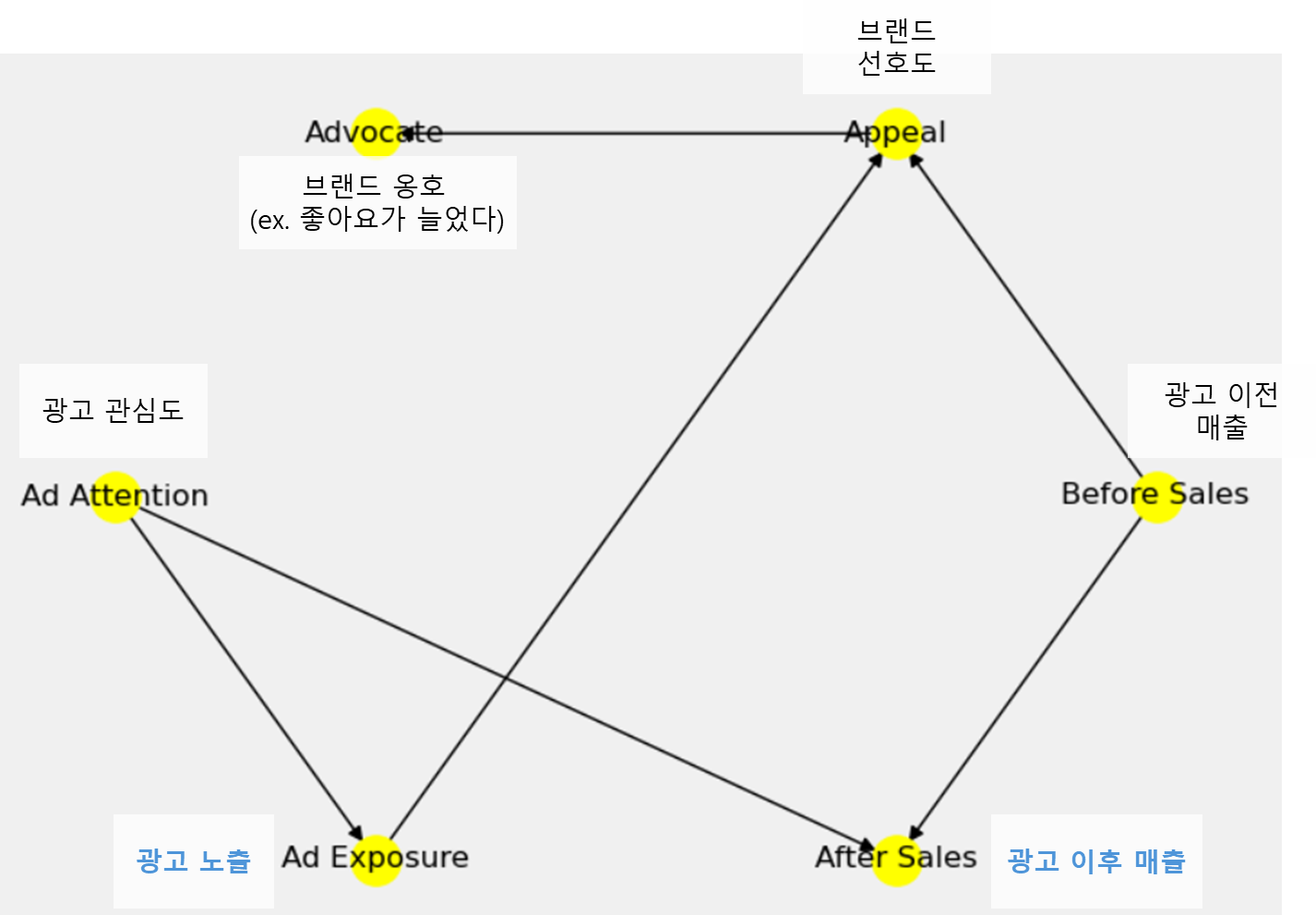
만일 광고 집행과 매출 간 다음과 같은 관계가 있다고 해보자! 우리는 이미 인과 그래프를 알고 있기 때문에 광고 노출이 매출에는 영향을 미치지 않는다는 슬픈 사실을 알고 있다. (광고 노출과 광고 이후 매출 사이에 직접적으로 연결되는 그래프가 없기 때문이다)
그런데 실제로는 광고 노출과 광고 이후 매출 간의 인과 관계를 알지 못하고, 대신 각 변수에 해당하는 데이터를 갖고 있다고 가정해 보자. 그러면 우리는 광고 이후 매출에 광고 노출이 미치는 영향을 판단하기 위해 어떤 변수를 넣어야 할까? 여기에 대한 답을 하기 위해 우리는 인과 그래프의 기본이 되는 3요소를 알아둬야 한다.
인과 그래프의 형태
인과 그래프에는 기본이 되는 Fork, Chain, Collider라는 3가지의 그래프 형태가 있다.

Fork

공통의 요소가 각 변수에 영향을 주는 그래프 모양을 의미한다. 이때 공통의 요소(위 그래프에서는 X 변수)를 Confounder라고 한다.
- X라는 변수가 Y, Z에 공통적으로 영향을 미치고 있기 때문에 X를 고려하지 않으면 Y와 Z는 서로 종속(dependent)이다.
- 그러나 X를 조건부로 두면, 즉 X 변수의 영향력을 통제한 상태에서는 Y와 Z는 서로 독립(independent)이다.
Chain

한 변수가 다른 변수에 영향을 주고, 다른 변수가 또 다른 변수에게 영향을 주는 형태의 그래프 모양을 의미한다. 줄줄이 소시지처럼 인과관계가 나타나는 것을 의미하는데 이때 중간의 매개 변수(위 그래프에서는 X 변수)를 Mediator라고도 부른다.
- Z가 X에 영향을 주고, 영향을 받은 X가 Y에 영향을 주기 때문에 X를 고려하지 않으면 Z와 Y 변수는 서로 종속(dependent)이다.
- 그러나 X를 조건부로 둔 상태에서는 Y와 Z는 서로 독립(independent)이다.
Collider
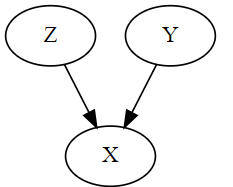
위에서 설명한 Fork와 모양이 유사하지만, 반대로 X 변수가 Y, Z 변수에 의해 영향을 받는 그래프 모양이다.
- Collider 관계가 있을 때, Z와 Y 변수는 서로 독립(independent)이다.
- 그러나 X를 조건부로 두면 이 때는 Z와 Y가 서로 종속(dependent)이 되어버린다. 독립적인 원인이 동일한 결과(collider)에 영향을 미치기 때문에 그 결과를 알면 원인들 간에 상관관계가 생기기 때문이다.
위 2개 그래프와는 다르게 Collider는 오히려 X 변수를 통제하면 없던 종속 관계가 생겨버린다. 예를 들어 Z = 2, Y = 5, X = 7이라는 인과 구조 방정식이 있다고 가정해 보자. 이때 X를 조건부로 두면, 즉 X = 7이라고 고정해 놓은 상태에서 Z가 2라는 것을 알면 자동으로 Y는 5라는 것을 알 수 있다. Z, Y가 서로 독립이라고 하더라도 2개 변수에 영향을 받는 다른 변수를 고정해 놓으면 하나의 변수를 알면 자연스럽게 다른 변수의 값을 알 수 있기 때문에 종속 관계가 발생한다.
d-분리
d-분리 (d-separation)는 주어진 경로(ex. X→Y)에서 특정 변수를 조건부로 놓을 때 X와 Y 사이의 모든 경로에서 인과 흐름이 차단되는 것을 의미한다. 좀 더 정확하게는 변수 간의 경로가 특정 조건에 의해 차단될 때 발생하는 독립성 조건을 의미한다.
만일 조건부 변수가 없거나 조건부 변수가 공집합인 경우 X와 Y는 무조건부 독립이 된다. 즉, d-분리가 되면 X와 Y는 조건부 독립(조건부 변수가 공집합이라면 무조건부 독립)이라고 해석할 수 있다. 반대로 특정 변수를 조건부로 두더라도 인과경로가 그대로 유지된다면 d-연결(d-connection)이라고 부른다. d-연결이 되었다면 X와 Y는 조건부 독립이 아니라고 말할 수 있다.
보다 정확하게 정의하게 위해 python 라이브러리의 networkx의 d-분리의 설명을 가져와 보았다.
d-separation is a test for conditional independence in probability distributions that can be factorized using DAGs.
지금까지 배웠던 그래프 3신기를 활용해서 d-분리가 되기 위한 조건을 구체적으로 표현해 볼 수 있다.
X와 Y가 d-분리되기 위해서는
- X와 Y의 경로에 있는 fork, chain을 조건부로 두거나,
- X와 Y의 경로에 있는 collider나 collider의 자손(descendent)을 조건부로 두면 안 된다.
- X와 Y의 경로에 있는 collider나 collider의 자손(descendent)을 조건부로 두면 종속 관계가 생겨 d-연결이 발생한다.
조금 더 첨언하면 fork와 chain 관계에 있는 변수를 조건부로 두면 조건부 독립이 되고, collider 관계에 있는 변수를 조건부로 두면 없던 관계가 생겨버린다. 그래서 d-분리를 만들기 위해서는 연결되는 경로 내에 fork와 chain은 조건부로 두되, collider는 건드리지 않는 편이 좋다는 것이다.
인과 그래프와 회귀분석
그럼 d-분리를 적용해서 아까의 그래프 예시를 다시 보도록 하자.
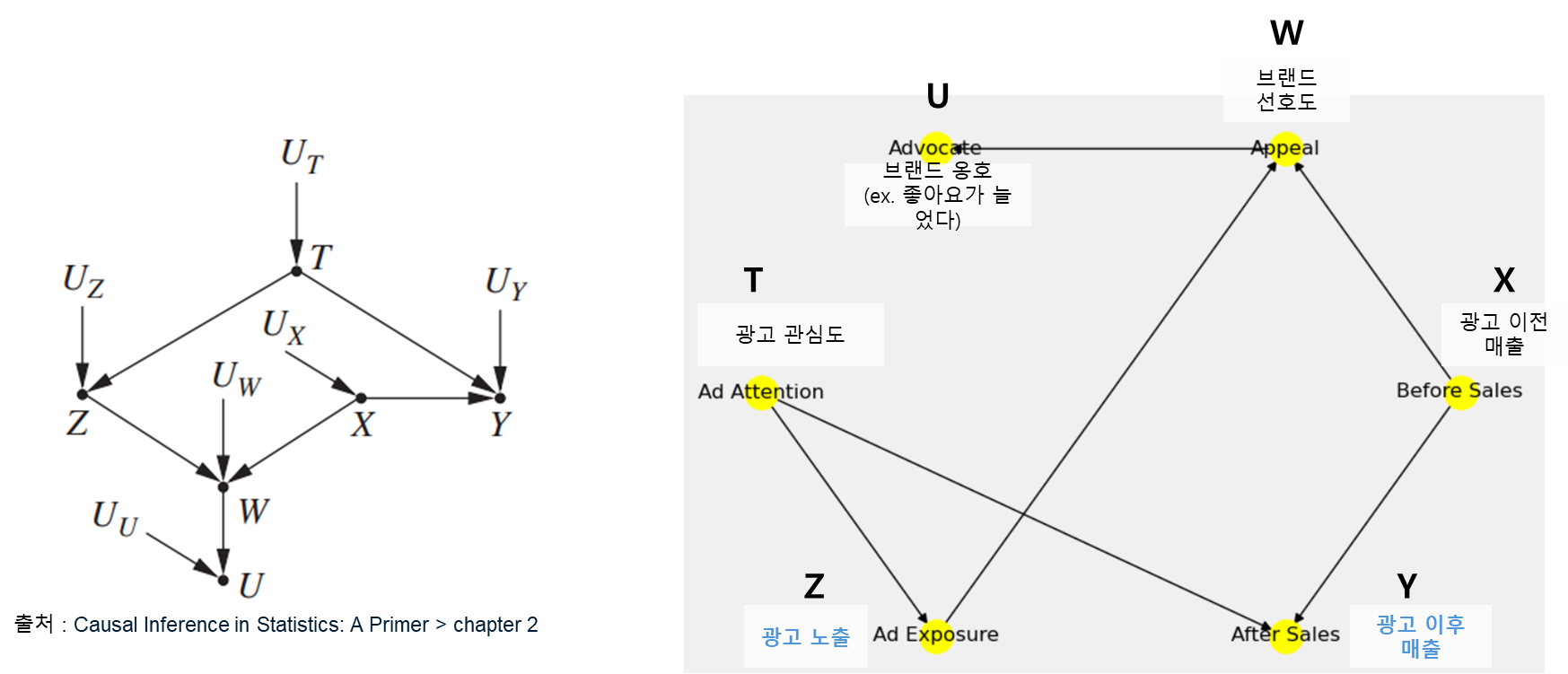
위의 예시는 사실 책에서 d-separation을 설명하는 그래프 예시 중 변수명만 현실에서 볼 법한 형태로 바꾼 것이다. 변수명이 긴 것보다는 X, Y, Z의 형태로 짧은 편이 부르기에 더 좋고, 예시가 그래프 형태(ex. fork, chain, collider)를 파악하기에 더 좋아 왼쪽의 그래프를 기준으로 설명을 첨언해보려 한다.
Z(광고 노출)과 Y(광고 이후 매출)은 직접 연결되는 경로 (Z→Y)가 없기 때문에 직접적인 인과관계가 있다고 보기는 어렵다.
다만 Z와 Y 사이에 2개 경로가 있는데, 그중 Z ← T → Y의 fork 경로로 인해 Z와 Y는 상관관계는 갖고 있다. 그래서 대충 보면 상관관계를 인과관계로 해석할 수 있어 유의해야 한다.
또 하나의 경로는 Z → W ← X → Y가 있는데, Z → W ← X가 collider이기 때문에 Z와 X는 독립이고, 이 경로에서는 Z와 Y는 자연스럽게 독립이 된다. 그런데 W(브랜드 선호도)나 U(브랜드 옹호) 변수를 조건부로 두면 어떻게 될까? Z와 Y 사이의 경로에 있는 collider를 조건부로 뒀기 때문에 오히려 독립 관계가 깨져버리게 되고 없던 허위 경로(spurious path)가 생기게 된다.
그러면 회귀분석으로 확인해 보자!
위의 그래프 형태를 표현해 주기 위해
- Z = 0.8T
- W = 0.6X
- Y = 0.7X + 0.8T
- W = 0.6X
- U = 0.43*W
의 수식을 사용해서 가상의 데이터를 만들었다.
우리가 궁금한 것은 Z가 Y에 미치는 영향력이다. 단, T로 인해 상관관계가 생겨버리므로 T를 통제해야 한다. 그러면 {Z, T} 변수를 넣고 회귀분석을 해보자.
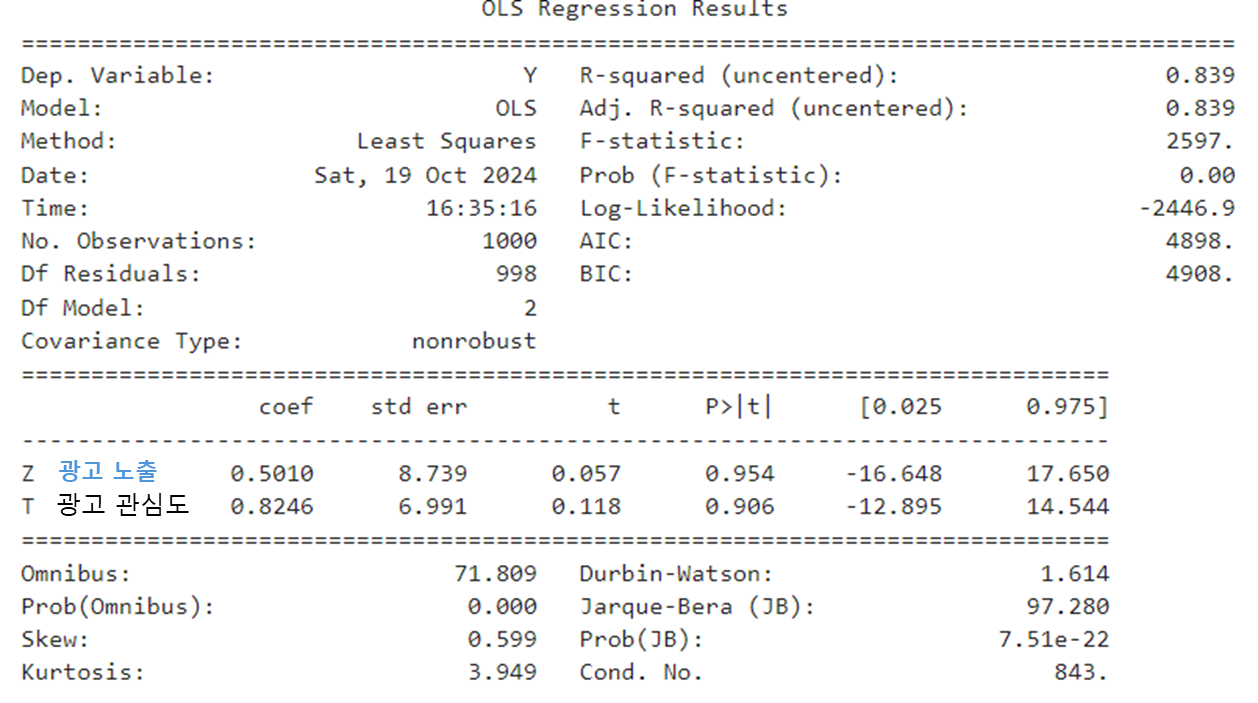
Z와 T 변수의 p-value가 모두 0.9 이상으로 나타나서 유의하지 않다는 결론이 나온다. 두둥. T는 Y에 직접 영향을 미치는 유의한 변수임에도 불구하고 X 변수가 누락되면서 T 변수의 coefficient에도 영향을 미친 것 같다. 그러나 처치 변수인 Z가 유의한 변수가 아니라는 해석이 나오므로 인과관계 자체는 제대로 해석이 되었다고 볼 수 있다.
그러면 이번에는 넣으면 안 된다고 말한 W, U 변수를 넣고 회귀분석을 돌려 보았다. 또, 반드시 조건부로 넣어야 하는 T 변수를 누락해 보았다.
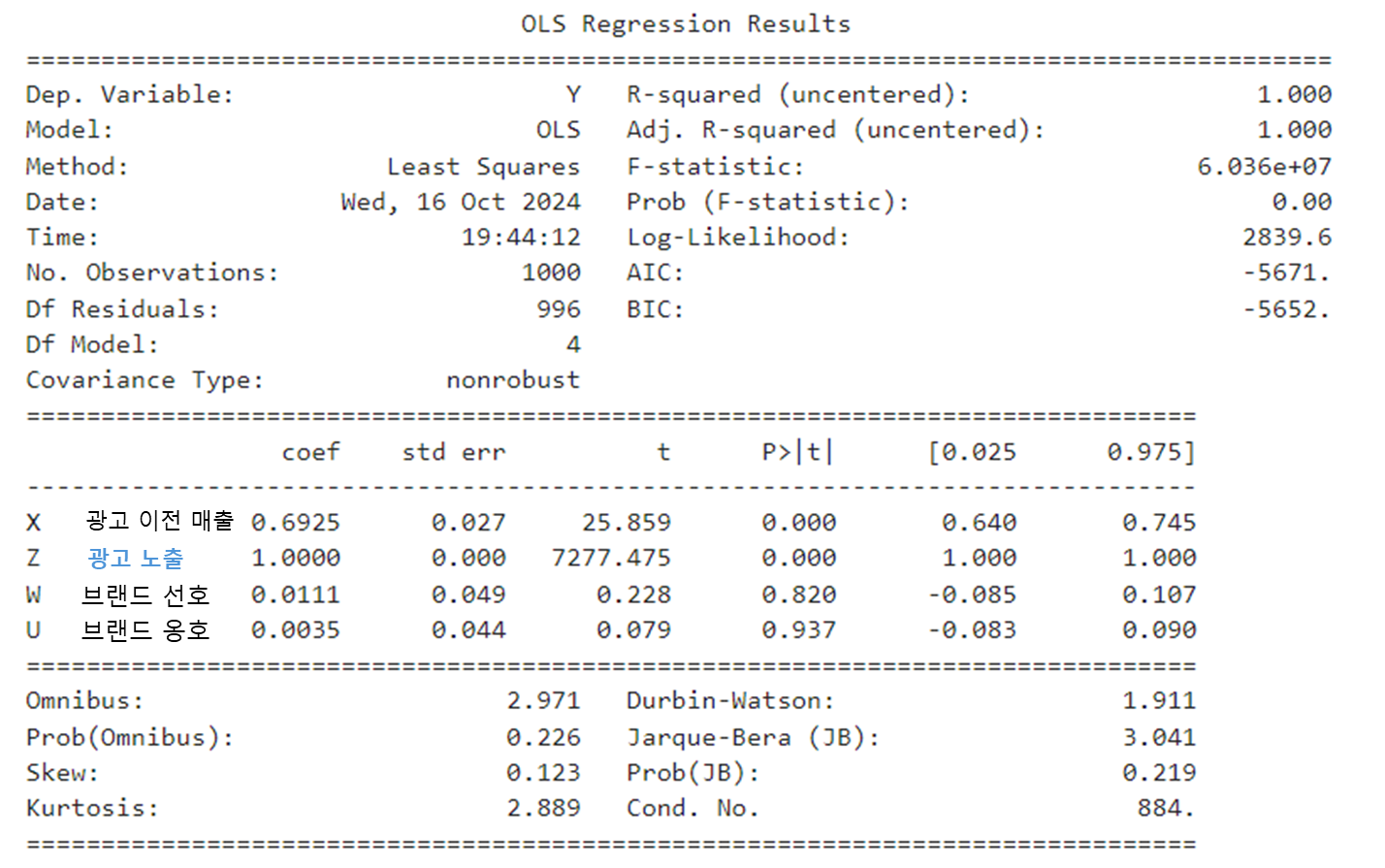
분명 Z는 유의한 변수가 아니어야 하는데, 이제는 p-value가 0.000이 되어 굉장히 유의한 변수가 되어버렸다. 앞서 말했듯 필수로 넣어야 하는 T 변수를 빼버리면서 없던 인과관계가 생겨버렸다. 또 엎친데 덮친 격으로 U, W와 같은 collider를 조건부로 두면서 허위 경로가 열리게 되었다.
이번에는 반드시 넣어야 하는 T 변수를 넣되, 넣으면 안 되는 변수인 U를 함께 넣어보았다.
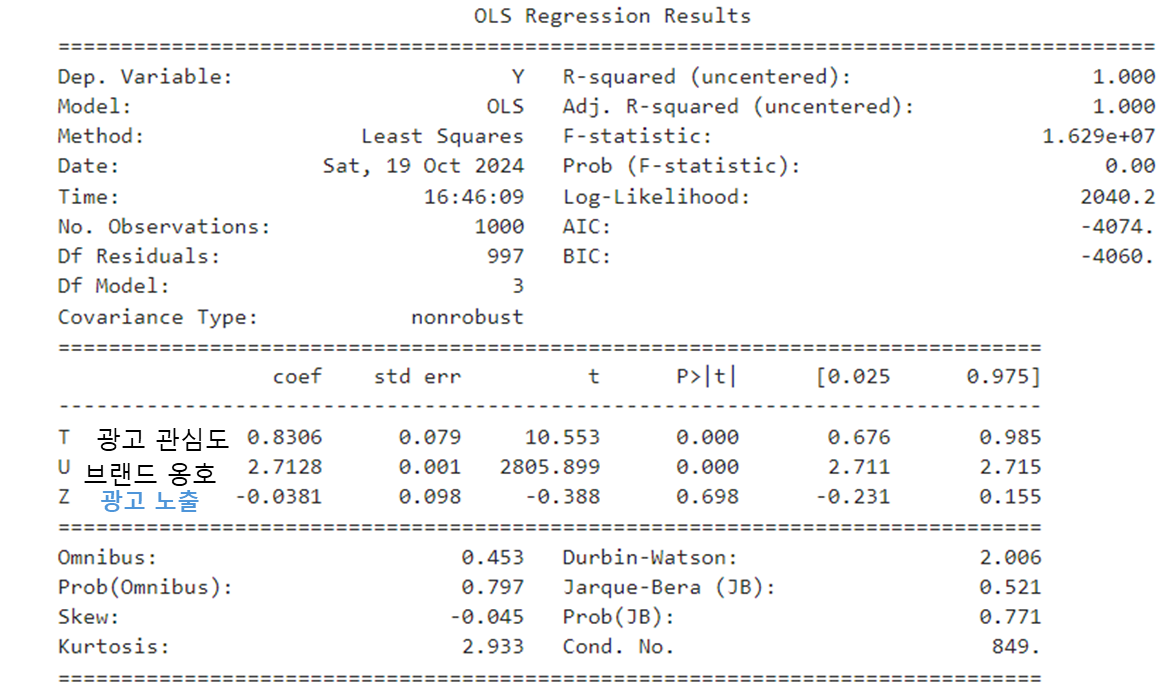
다행히 Z 변수는 p-value가 0.698로 유의하지 않다고 나오기는 하지만, 이건 운이 좋았을 뿐이다. (Z 변수가 유의하게 바뀌었으면 그림이 좋았을 뻔했는데... 아깝다.) 논외로 Y 변수에 영향을 받는 U 변수가 굉장히 유의한 변수가 되어버렸다.
만약에 collider를 반드시 모형에 넣고 싶다고 하면 어떨까. 이때 collider와 함께 X 변수를 통제해 주면 된다. collider를 넣어 허위 경로가 생기더라도 허위경로를 받는 X 변수까지 같이 통제해 주면 다시 경로가 차단되기 때문이다.
마지막으로 반드시 넣어야 하는 T 변수, collider인 U 변수, 가상의 허위 경로를 차단해 주기 위한 X 변수를 회귀모형에 넣어보자.
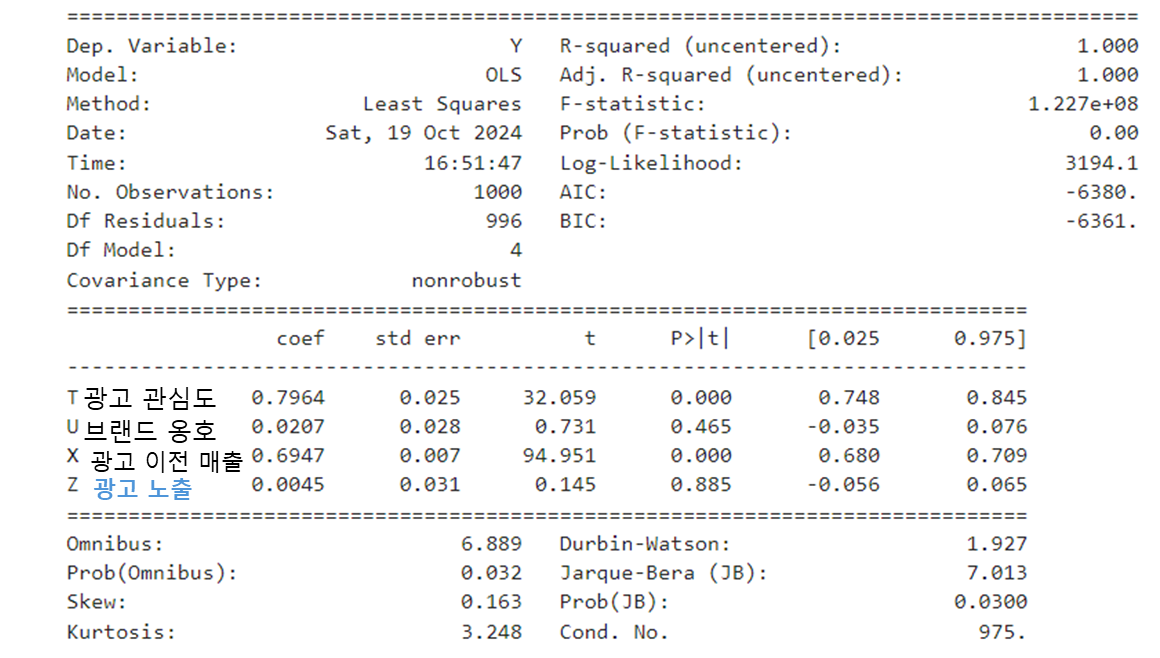
비로소 제대로 된 인과관계를 포착해 냈다! Y = 0.8*T + 0.7*X라는 원래의 회귀식대로 coefficient가 도출됐으며 collider인 U 변수는 유의하지 않게 되었고, Z 변수도 유의하지 않게 되었다.
만일 단순 예측 모형을 만든다면 다양한 변수를 넣고 예측력이 높은 모형을 선택했으면 됐을지도 모른다. 그러나 인과관계를 포착하기 위해서는 변수 간 관계를 고려하는 것이 중요하다. 그렇지 않으면 존재하지 않아야 할 인과관계가 생겨 잘못된 해석을 할 수 있기 때문이다.
그래서 인과 그래프를 그려보며 미리 인과관계에 대한 가설을 세워보는 게 중요하고, 그러기 위해서는 인과 그래프에 대한 이해가 중요하다. 또 무엇보다 인과 그래프에 대한 가설을 세울 수 있도록 "도메인" 지식을 갖추는 것이 매우 중요하다고 볼 수 있겠다.
참고자료
Causal Inference in Statistics: A Primer
(참고) 회귀분석에 사용한 코드
그래프 생성에 인과관계 추론과 발견 책을 참고하였다.
# 라이브러리
import numpy as np
import pandas as pd
from scipy import stats
import dowhy
from dowhy import CausalModel
import graphviz
# 인과그래프 구성
# Create the graph describing the causal structure
gml_graph = """
graph [
directed 1
node [
id "T"
label "Ad Attention"
]
node [
id "Z"
label "Ad Exposure"
]
node [
id "Y"
label "After Sales"
]
node [
id "X"
label "Before Sales"
]
node [
id "W"
label "Appeal"
]
node [
id "U"
label "Advocate"
]
edge [
source "T"
target "Z"
]
edge [
source "T"
target "Y"
]
edge [
source "X"
target "Y"
]
edge [
source "X"
target "W"
]
edge [
source "W"
target "U"
]
edge [
source "Z"
target "W"
]
]
"""
# 시뮬레이션 데이터 생성
SAMPLE_SIZE = 1000
T = stats.truncnorm(0, np.infty, scale = 5).rvs(SAMPLE_SIZE)
X = stats.truncnorm(0, np.infty, scale = 5).rvs(SAMPLE_SIZE)
Z = 0.8*T +0.01*np.random.normal(size = SAMPLE_SIZE)
W = 0.6*X +0.01*np.random.normal(size = SAMPLE_SIZE)
Y = 0.7*X + 0.8*T +0.01*np.random.normal(size = SAMPLE_SIZE)
U = 0.43*W + 0.01*np.random.normal(size = SAMPLE_SIZE)
df = pd.DataFrame(np.vstack([T, X, Z, W, Y, U]).T, columns=['T', 'X', 'Z', 'W', 'Y', 'U'])
# 인과 그래프 생성
model = CausalModel(
data=df,
treatment='Z',
outcome='Y',
graph=gml_graph
)
model.view_model()
# 회귀분석
import statsmodels.api as sm
# 마지막 회귀분석만 대표로
outcome = df['Y']
dependent_var4 = df[['T', 'U', 'X','Z']]
lm_model4 = sm.OLS(outcome, dependent_var4)
res4 = lm_model4.fit()
print(res4.summary())'Statistics' 카테고리의 다른 글
| 가상의 게임 데이터로 살펴보는 이중차분법 (feat. 🧙♂️법사야캐요) (0) | 2024.12.30 |
|---|---|
| 인과추론 학습기 - 개입과 뒷문 기준 (2) | 2024.11.01 |
| 인과추론을 위한 회귀분석 개념 정리 - 편회귀계수, FWL 정리 (2) | 2024.04.21 |
| 매칭(Matching)을 통한 인과추론 : 개념부터 실습까지 (feat. ChatGPT) (2) | 2024.03.25 |
| 꼬리에 꼬리를 무는 시계열 개념 정리, 정상성부터 공적분까지 (4) | 2024.01.14 |
오늘은 인과추론의 주요 개념 중 하나인 인과 그래프에 대한 글을 써보려고 한다.
- 독립, 조건부 독립 등 기초 통계
- 회귀분석에 대한 개념을 미리 알고 있어야 글을 이해하기 편할 것 같다.
글에서는 다루지는 않지만, 베이지안 통계에 대한 이해도가 있으면 아래 설명을 기반으로 심화된 내용을 확장해서 찾아보기 편할 것 같다.
기본 용어
SCM (Structural Causal Model)
한글로 그대로 직역하면 구조화된 인과모형이다. 즉, 인과관계를 구조적으로 설명하는 모델로서, 좀 더 자세히 말하면 변수 간의 인과 관계를 명시적으로 수식화하여 표현하는 모델이다. 이러한 모형을 사용하면 인과 관계의 방향성과 크기를 명확히 이해할 수 있다.
예를 들어 하루 섭취한 칼로리가 500kcal를 넘어갈 때마다 체중 1kg가 증가한다고 가정해 보자.(슬픈 가정이지만..)
그러면 증가한 체중(\(Y\)) := 500 * 초과 섭취한 칼로리(\(X\))라는 수식을 쓸 수 있다.
인과관계를 이렇게 수식으로 표현하는 것을 SCM이라고 한다.
외생변수, 내생변수
위의 관계 Y = 500*X라는 수식에서 체중(Y) 변수는 내생변수이다. 내생변수는 인과 모형 안에서 다른 변수에 의해 영향을 받는 변수, 즉, 인과 관계를 설명하는 데 사용되는 변수라는 의미이다. 칼로리 초과 섭취에 의해 체중의 변동이 일어나기 때문에 체중은 내생변수가 된다.
반면, 인과 모형 밖에서 결정되는 변수도 있다. 이를 외생변수라고 한다. 예를 들어 가을이 되면서 식욕이 늘어 섭취 칼로리가 늘었다고 해보자. 가을이라는 "계절"은 섭취 칼로리에 영향을 줄 수 있지만, 인과 모형(섭취칼로리와 체중이라는 인과모형) 밖에서 이미 결정된 변수이기 때문에 이를 외생변수라 부를 수 있게 된다.
잠깐 딴 소리를 하자면 위에서 말하는 외생변수, 내생변수는 회귀분석에서 말하는 내생성(endogeneity) 문제와 조금 결이 다르다. 회귀분석에서 말하는 내생성은 설명변수(독립변수)와 잔차 간에 상관성이 생기는 현상을 의미한다. 주로 누락된 변수(omitted variable problem 이라고도 한다.)나 잘못된 변수를 넣을 때 발생할 수 있다.
즉, 잔차항과 상관관계를 갖는 변수를 내생변수라고 하고, 그렇지 않은 변수를 외생변수라고 한다. (조금 딴 소리지만 외생변수에 대한 정의가 인과 그래프와 회귀분석에 조금 차이가 있어 첨언해 보았다.)
주요 그래프 용어

위에서 설명한 SCM을 기반으로 인과 그래프를 그릴 수 있다. 인과 그래프라고 하면 거창해 보이는데,
- 영향을 받는 변수를 화살표를 받는 쪽으로,
- 영향을 주는 변수를 화살표를 주는 쪽으로 놓고 그래프를 그리면 그게 인과 그래프다.
그리고 영향을 주고받는 각 변수를 노드(Node)로, 변수 간 관계를 엣지(Edge)라고 부른다.
그리고 보통 인과관계를 표현할 때 사용하는 그래프는 DAG (Directed Acyclic Graph) 형태를 지닌다. DAG라고 하니 이것도 마찬가지로 굉장히 거창해 보이지만, 직독직해하자면
- Directed : 방향성이 있고 (화살표가 포함되는 그래프)
- Acyclic : 순환하지 않는
- Graph : 그래프
라는 의미이다.
즉, X가 Y에 영향을 준다는 관계성을 표현해야 하기 때문에 화살표(방향성)가 필요하다. 또한, X가 Y에 영향을 주면서 Y가 X에 주는 순환관계(인과관계 - 역 인과관계 동시 성립)는 발생하지 않아야 한다.
인과 그래프가 중요한 이유
여기까지 신나게 SCM과 인과그래프에 대해 이야기했다. 인과 그래프가 회귀분석, 머신러닝 같은 분석에 사용되는 기법은 아니기 때문에 멋이 없어 보일 수도 있다. (사실 내가 처음 공부할 때 그랬음)
그런데 인과 그래프를 그려보는 것은 분석 기법을 적용하기 전에 거의 무조건 선행되어야 한다! 그렇지 않으면 소위 Bad Control 문제가 나타날 수 있기 때문이다.
회귀분석에 대해 배울 때 설명변수를 가려 넣으세요 와 같은 이야기를 들은 적이 있을까? 아마 다중공선성 문제가 없거나 과적합 문제가 없다는 가정 하에서 다양한 설명변수를 많이 넣고 보는 게 좋다고 배웠을 가능성이 클 것 같다. 예측문제에서는 쓸 수 있는 변수가 많은 것이 선(善)이라고 볼 수 있지만, 인과 관계를 추론할 때는 아무 변수나 막 넣으면 오히려 인과관계를 왜곡하여 해석할 수 있는 여지가 발생한다.

만일 광고 집행과 매출 간 다음과 같은 관계가 있다고 해보자! 우리는 이미 인과 그래프를 알고 있기 때문에 광고 노출이 매출에는 영향을 미치지 않는다는 슬픈 사실을 알고 있다. (광고 노출과 광고 이후 매출 사이에 직접적으로 연결되는 그래프가 없기 때문이다)
그런데 실제로는 광고 노출과 광고 이후 매출 간의 인과 관계를 알지 못하고, 대신 각 변수에 해당하는 데이터를 갖고 있다고 가정해 보자. 그러면 우리는 광고 이후 매출에 광고 노출이 미치는 영향을 판단하기 위해 어떤 변수를 넣어야 할까? 여기에 대한 답을 하기 위해 우리는 인과 그래프의 기본이 되는 3요소를 알아둬야 한다.
인과 그래프의 형태
인과 그래프에는 기본이 되는 Fork, Chain, Collider라는 3가지의 그래프 형태가 있다.

Fork

공통의 요소가 각 변수에 영향을 주는 그래프 모양을 의미한다. 이때 공통의 요소(위 그래프에서는 X 변수)를 Confounder라고 한다.
- X라는 변수가 Y, Z에 공통적으로 영향을 미치고 있기 때문에 X를 고려하지 않으면 Y와 Z는 서로 종속(dependent)이다.
- 그러나 X를 조건부로 두면, 즉 X 변수의 영향력을 통제한 상태에서는 Y와 Z는 서로 독립(independent)이다.
Chain

한 변수가 다른 변수에 영향을 주고, 다른 변수가 또 다른 변수에게 영향을 주는 형태의 그래프 모양을 의미한다. 줄줄이 소시지처럼 인과관계가 나타나는 것을 의미하는데 이때 중간의 매개 변수(위 그래프에서는 X 변수)를 Mediator라고도 부른다.
- Z가 X에 영향을 주고, 영향을 받은 X가 Y에 영향을 주기 때문에 X를 고려하지 않으면 Z와 Y 변수는 서로 종속(dependent)이다.
- 그러나 X를 조건부로 둔 상태에서는 Y와 Z는 서로 독립(independent)이다.
Collider

위에서 설명한 Fork와 모양이 유사하지만, 반대로 X 변수가 Y, Z 변수에 의해 영향을 받는 그래프 모양이다.
- Collider 관계가 있을 때, Z와 Y 변수는 서로 독립(independent)이다.
- 그러나 X를 조건부로 두면 이 때는 Z와 Y가 서로 종속(dependent)이 되어버린다. 독립적인 원인이 동일한 결과(collider)에 영향을 미치기 때문에 그 결과를 알면 원인들 간에 상관관계가 생기기 때문이다.
위 2개 그래프와는 다르게 Collider는 오히려 X 변수를 통제하면 없던 종속 관계가 생겨버린다. 예를 들어 Z = 2, Y = 5, X = 7이라는 인과 구조 방정식이 있다고 가정해 보자. 이때 X를 조건부로 두면, 즉 X = 7이라고 고정해 놓은 상태에서 Z가 2라는 것을 알면 자동으로 Y는 5라는 것을 알 수 있다. Z, Y가 서로 독립이라고 하더라도 2개 변수에 영향을 받는 다른 변수를 고정해 놓으면 하나의 변수를 알면 자연스럽게 다른 변수의 값을 알 수 있기 때문에 종속 관계가 발생한다.
d-분리
d-분리 (d-separation)는 주어진 경로(ex. X→Y)에서 특정 변수를 조건부로 놓을 때 X와 Y 사이의 모든 경로에서 인과 흐름이 차단되는 것을 의미한다. 좀 더 정확하게는 변수 간의 경로가 특정 조건에 의해 차단될 때 발생하는 독립성 조건을 의미한다.
만일 조건부 변수가 없거나 조건부 변수가 공집합인 경우 X와 Y는 무조건부 독립이 된다. 즉, d-분리가 되면 X와 Y는 조건부 독립(조건부 변수가 공집합이라면 무조건부 독립)이라고 해석할 수 있다. 반대로 특정 변수를 조건부로 두더라도 인과경로가 그대로 유지된다면 d-연결(d-connection)이라고 부른다. d-연결이 되었다면 X와 Y는 조건부 독립이 아니라고 말할 수 있다.
보다 정확하게 정의하게 위해 python 라이브러리의 networkx의 d-분리의 설명을 가져와 보았다.
d-separation is a test for conditional independence in probability distributions that can be factorized using DAGs.
지금까지 배웠던 그래프 3신기를 활용해서 d-분리가 되기 위한 조건을 구체적으로 표현해 볼 수 있다.
X와 Y가 d-분리되기 위해서는
- X와 Y의 경로에 있는 fork, chain을 조건부로 두거나,
- X와 Y의 경로에 있는 collider나 collider의 자손(descendent)을 조건부로 두면 안 된다.
- X와 Y의 경로에 있는 collider나 collider의 자손(descendent)을 조건부로 두면 종속 관계가 생겨 d-연결이 발생한다.
조금 더 첨언하면 fork와 chain 관계에 있는 변수를 조건부로 두면 조건부 독립이 되고, collider 관계에 있는 변수를 조건부로 두면 없던 관계가 생겨버린다. 그래서 d-분리를 만들기 위해서는 연결되는 경로 내에 fork와 chain은 조건부로 두되, collider는 건드리지 않는 편이 좋다는 것이다.
인과 그래프와 회귀분석
그럼 d-분리를 적용해서 아까의 그래프 예시를 다시 보도록 하자.

위의 예시는 사실 책에서 d-separation을 설명하는 그래프 예시 중 변수명만 현실에서 볼 법한 형태로 바꾼 것이다. 변수명이 긴 것보다는 X, Y, Z의 형태로 짧은 편이 부르기에 더 좋고, 예시가 그래프 형태(ex. fork, chain, collider)를 파악하기에 더 좋아 왼쪽의 그래프를 기준으로 설명을 첨언해보려 한다.
Z(광고 노출)과 Y(광고 이후 매출)은 직접 연결되는 경로 (Z→Y)가 없기 때문에 직접적인 인과관계가 있다고 보기는 어렵다.
다만 Z와 Y 사이에 2개 경로가 있는데, 그중 Z ← T → Y의 fork 경로로 인해 Z와 Y는 상관관계는 갖고 있다. 그래서 대충 보면 상관관계를 인과관계로 해석할 수 있어 유의해야 한다.
또 하나의 경로는 Z → W ← X → Y가 있는데, Z → W ← X가 collider이기 때문에 Z와 X는 독립이고, 이 경로에서는 Z와 Y는 자연스럽게 독립이 된다. 그런데 W(브랜드 선호도)나 U(브랜드 옹호) 변수를 조건부로 두면 어떻게 될까? Z와 Y 사이의 경로에 있는 collider를 조건부로 뒀기 때문에 오히려 독립 관계가 깨져버리게 되고 없던 허위 경로(spurious path)가 생기게 된다.
그러면 회귀분석으로 확인해 보자!
위의 그래프 형태를 표현해 주기 위해
- Z = 0.8T
- W = 0.6X
- Y = 0.7X + 0.8T
- W = 0.6X
- U = 0.43*W
의 수식을 사용해서 가상의 데이터를 만들었다.
우리가 궁금한 것은 Z가 Y에 미치는 영향력이다. 단, T로 인해 상관관계가 생겨버리므로 T를 통제해야 한다. 그러면 {Z, T} 변수를 넣고 회귀분석을 해보자.

Z와 T 변수의 p-value가 모두 0.9 이상으로 나타나서 유의하지 않다는 결론이 나온다. 두둥. T는 Y에 직접 영향을 미치는 유의한 변수임에도 불구하고 X 변수가 누락되면서 T 변수의 coefficient에도 영향을 미친 것 같다. 그러나 처치 변수인 Z가 유의한 변수가 아니라는 해석이 나오므로 인과관계 자체는 제대로 해석이 되었다고 볼 수 있다.
그러면 이번에는 넣으면 안 된다고 말한 W, U 변수를 넣고 회귀분석을 돌려 보았다. 또, 반드시 조건부로 넣어야 하는 T 변수를 누락해 보았다.

분명 Z는 유의한 변수가 아니어야 하는데, 이제는 p-value가 0.000이 되어 굉장히 유의한 변수가 되어버렸다. 앞서 말했듯 필수로 넣어야 하는 T 변수를 빼버리면서 없던 인과관계가 생겨버렸다. 또 엎친데 덮친 격으로 U, W와 같은 collider를 조건부로 두면서 허위 경로가 열리게 되었다.
이번에는 반드시 넣어야 하는 T 변수를 넣되, 넣으면 안 되는 변수인 U를 함께 넣어보았다.

다행히 Z 변수는 p-value가 0.698로 유의하지 않다고 나오기는 하지만, 이건 운이 좋았을 뿐이다. (Z 변수가 유의하게 바뀌었으면 그림이 좋았을 뻔했는데... 아깝다.) 논외로 Y 변수에 영향을 받는 U 변수가 굉장히 유의한 변수가 되어버렸다.
만약에 collider를 반드시 모형에 넣고 싶다고 하면 어떨까. 이때 collider와 함께 X 변수를 통제해 주면 된다. collider를 넣어 허위 경로가 생기더라도 허위경로를 받는 X 변수까지 같이 통제해 주면 다시 경로가 차단되기 때문이다.
마지막으로 반드시 넣어야 하는 T 변수, collider인 U 변수, 가상의 허위 경로를 차단해 주기 위한 X 변수를 회귀모형에 넣어보자.

비로소 제대로 된 인과관계를 포착해 냈다! Y = 0.8*T + 0.7*X라는 원래의 회귀식대로 coefficient가 도출됐으며 collider인 U 변수는 유의하지 않게 되었고, Z 변수도 유의하지 않게 되었다.
만일 단순 예측 모형을 만든다면 다양한 변수를 넣고 예측력이 높은 모형을 선택했으면 됐을지도 모른다. 그러나 인과관계를 포착하기 위해서는 변수 간 관계를 고려하는 것이 중요하다. 그렇지 않으면 존재하지 않아야 할 인과관계가 생겨 잘못된 해석을 할 수 있기 때문이다.
그래서 인과 그래프를 그려보며 미리 인과관계에 대한 가설을 세워보는 게 중요하고, 그러기 위해서는 인과 그래프에 대한 이해가 중요하다. 또 무엇보다 인과 그래프에 대한 가설을 세울 수 있도록 "도메인" 지식을 갖추는 것이 매우 중요하다고 볼 수 있겠다.
참고자료
Causal Inference in Statistics: A Primer
(참고) 회귀분석에 사용한 코드
그래프 생성에 인과관계 추론과 발견 책을 참고하였다.
# 라이브러리
import numpy as np
import pandas as pd
from scipy import stats
import dowhy
from dowhy import CausalModel
import graphviz
# 인과그래프 구성
# Create the graph describing the causal structure
gml_graph = """
graph [
directed 1
node [
id "T"
label "Ad Attention"
]
node [
id "Z"
label "Ad Exposure"
]
node [
id "Y"
label "After Sales"
]
node [
id "X"
label "Before Sales"
]
node [
id "W"
label "Appeal"
]
node [
id "U"
label "Advocate"
]
edge [
source "T"
target "Z"
]
edge [
source "T"
target "Y"
]
edge [
source "X"
target "Y"
]
edge [
source "X"
target "W"
]
edge [
source "W"
target "U"
]
edge [
source "Z"
target "W"
]
]
"""
# 시뮬레이션 데이터 생성
SAMPLE_SIZE = 1000
T = stats.truncnorm(0, np.infty, scale = 5).rvs(SAMPLE_SIZE)
X = stats.truncnorm(0, np.infty, scale = 5).rvs(SAMPLE_SIZE)
Z = 0.8*T +0.01*np.random.normal(size = SAMPLE_SIZE)
W = 0.6*X +0.01*np.random.normal(size = SAMPLE_SIZE)
Y = 0.7*X + 0.8*T +0.01*np.random.normal(size = SAMPLE_SIZE)
U = 0.43*W + 0.01*np.random.normal(size = SAMPLE_SIZE)
df = pd.DataFrame(np.vstack([T, X, Z, W, Y, U]).T, columns=['T', 'X', 'Z', 'W', 'Y', 'U'])
# 인과 그래프 생성
model = CausalModel(
data=df,
treatment='Z',
outcome='Y',
graph=gml_graph
)
model.view_model()
# 회귀분석
import statsmodels.api as sm
# 마지막 회귀분석만 대표로
outcome = df['Y']
dependent_var4 = df[['T', 'U', 'X','Z']]
lm_model4 = sm.OLS(outcome, dependent_var4)
res4 = lm_model4.fit()
print(res4.summary())'Statistics' 카테고리의 다른 글
| 가상의 게임 데이터로 살펴보는 이중차분법 (feat. 🧙♂️법사야캐요) (0) | 2024.12.30 |
|---|---|
| 인과추론 학습기 - 개입과 뒷문 기준 (2) | 2024.11.01 |
| 인과추론을 위한 회귀분석 개념 정리 - 편회귀계수, FWL 정리 (2) | 2024.04.21 |
| 매칭(Matching)을 통한 인과추론 : 개념부터 실습까지 (feat. ChatGPT) (2) | 2024.03.25 |
| 꼬리에 꼬리를 무는 시계열 개념 정리, 정상성부터 공적분까지 (4) | 2024.01.14 |
