배경
최근 매칭을 업무에 오랜만에 써보는 일이 있었다. 오랜만에 써봐서 잊고 있었는데 매칭은 은근 분석에 도움이 되어, 가끔씩이라도 쓰게 되는 일이 있는 것 같다는 생각이 들었다. 향후 다시 매칭을 써먹을 나를 위해, 그리고 매칭을 적용해보고 싶은 사람들을 위해 정리할 겸 글을 남기게 되었다.
글은 매칭의 개념, 매칭의 한계, 매칭 방법에 대한 간단한 소개, 매칭에 사용하는 코드(R 위주) 순으로 진행하려 한다.

매칭의 개념 및 목적
매칭은 간단히 말하면 Treatment 그룹(처치군 ; 처치를 받은 대상)과 Control 그룹(대조군 ; 처치를 받지 않은 대상) 간 특성이 비슷한 사람을 짝지어주는 것을 의미한다.
이러한 짝짓기가 필요한 이유는 Selection Bias(선택 편향) 때문인데, 선택 편향의 정의를 살펴보면 다음과 같다.
선택 편향(영어: selection bias) 또는 선택적 보고(영어: selective reporting)는 표본을 사전 또는 사후 선택함에 따라 통계 분석을 왜곡하는 오류다. 일반적으로 이것은 통계적 유의성의 척도를 실제보다 더 크게 나타나도록 만든다.
출처 : 위키백과
예를 들어 선택 편향을 고려하지 않으면 병원에 입원한 사람이 그렇지 않은 사람보다 건강 정도가 더 나쁘기 때문에 병원 입원이 건강 악화를 야기한다는 잘못된 결과를 낼 수 있다. 병원에 입원하는 사람은 건강이 매우 나빠졌기 때문에 입원하는 경우가 일반적이므로, 단순히 입원한 사람과 그렇지 않은 사람을 비교하는 것은 올바르지 않다는 의미이다.
매칭의 전략은 Covariate(공변량)이 비슷한 사람끼리 짝짓고, 비슷한 사람까리만 Outcome variable(우리가 보려고 하는 성과변수, 위의 예시에서는 건강 상태)를 비교하여 Selection Bias를 줄이려고 하는 것이다. 위의 예시 기준으로는 성별 / 흡연 여부 / 음주 여부 / 주 운동 횟수 / 이전 병력 등이 비슷한 사람 중에 병원 입원을 택한 그룹(Treatment)과 방문 진료를 택한 그룹(Control)의 진료 이후의 건강 상태를 비교해야만 올바른 비교가 될 수 있는 뜻이다.

회귀분석과의 공통점/차이점
공변량(Covariate)이 비슷한 사람끼리 짝짓는다는 점에서 매칭은 회귀분석(Regression)과 비교가 가능하다. 회귀분석 역시 성과변수(Outcome Variable)에 영향을 미치는 요인으로 처치변수(Treatment Variable)과 공변량(Covariate)를 같이 활용할 수 있다. 다시 말해 공변량(Covariate)이 통제된 상태에서 처치 효과(Treatment Effect)를 비교한다는 측면에서 매칭과 회귀분석은 공통점을 갖고 있다.
대체로 해롭지 않은 경제학에서는 회귀분석 역시 특수한 형태의 매칭이라고 언급하기도 하는데, 이는 회귀분석 역시 매칭의 한 범주에 들어갈 수 있음을 의미한다.
그렇지만 회귀분석과 매칭은 차이가 있다. 먼저 처치효과(Treatment Effect)를 구하는 방식에 차이가 있다. 매칭의 경우, 처치(Treatment)를 받을 가능성이 높은 공변량(Covariate)에 더 큰 가중치를 부여한다. 그렇지만 회귀분석은 \(Cov(X,\tilde{D})/Var(\tilde{D})\) 이 큰 쪽, 즉 조건부 분산이 더 큰 가중치를 부여한다.
회귀분석은 회귀식(Functional Form)에 크게 의존한다. 회귀 식에 변수 간 상호작용(interaction)을 고려할 것인지, N차항을 고려할 것인지에 따라 처치효과(Treatment Effect)가 달라지게 된다. 반면 매칭은 꼭 회귀식의 형태가 아니더라도 처치그룹(Treatment)과 대조군(Control)을 비교할 수 있다. 즉, Functional Form에 대한 의존도가 회귀분석보다는 낮은 편이다.
매칭의 한계점
매칭도, 회귀분석도 모두 공통적인 한계가 있다. 공변량(Covariate)을 통제해서 선택 편향(Selection Bias)을 제거하는 전략은 통제해야 할 공변량을 빼먹게 된다면 여전히 선택 편향이 남아버리는 맹점이 있다.
"노력하면 성공한다"라는 문장을 인과적으로 분석한다고 가정해보자. 일단 "노력"과 "성공"이라는 걸 정량화할 수 있는지는 차치하더라도, 그래서 나름대로 노력과 성공을 정량화할 수 있는 기준을 찾아내더라도 "노력하는 사람"과 "노력하지 않는 사람"을 온전히 비교하기는 어렵다.


"노력"이라는 것도 타고난 유전이나 재능이라고 이야기하는 경우를 꽤 많이 봤다. 논의가 거기에만 그치면 다행이지만, 정말 슬프게도 내가 노력하지 않는 건 노력이라는 재능을 타고나지 못했다고 아예 시도도 하지 않고 손을 놔버리는 경우가 있다고도 들었다.
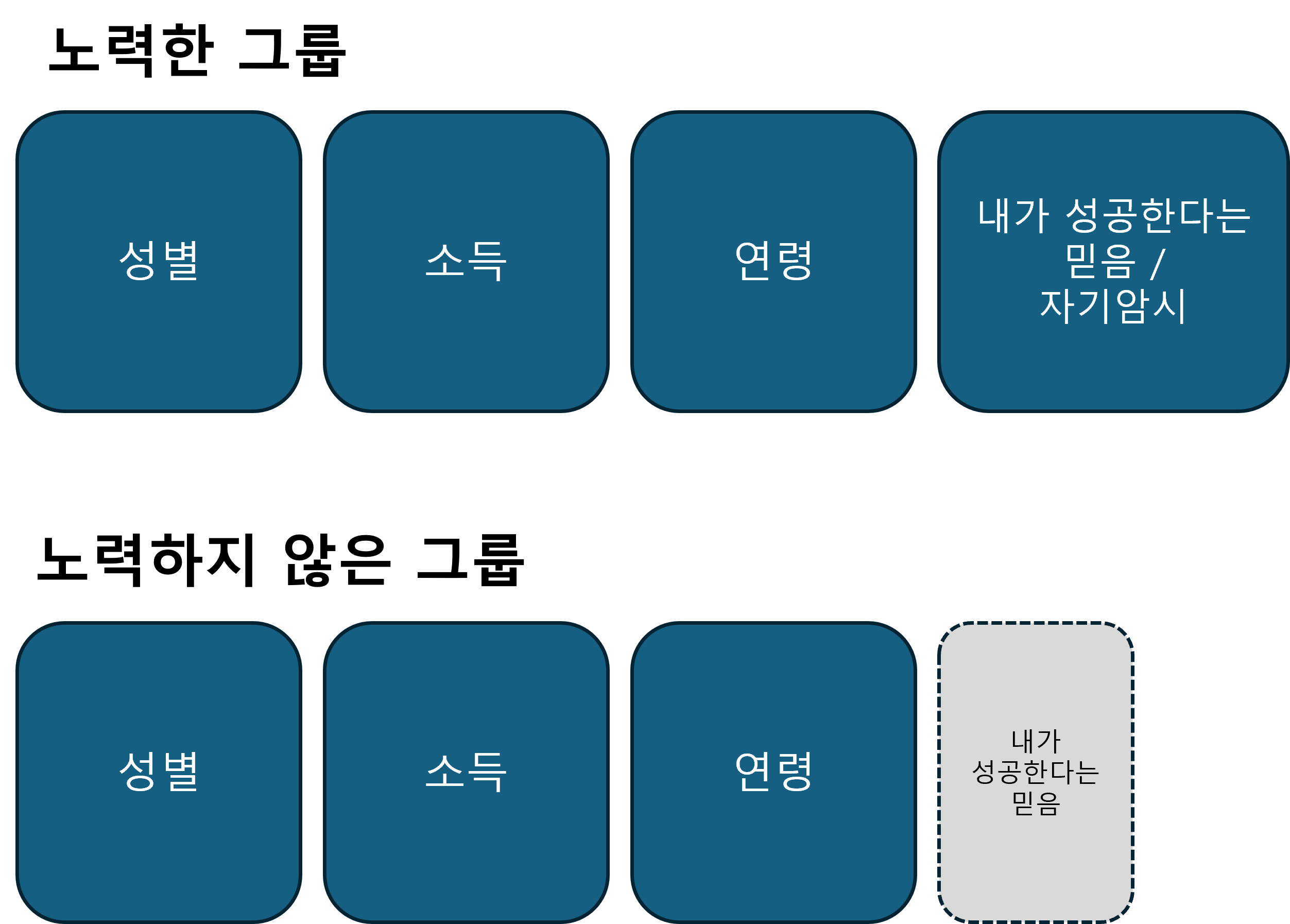
굳이 뭔가 분석하지 않아도, 상식적으로는 노력하는 쪽이 노력하지 않은 쪽보다 더 성공할 확률이 높을 것이다. 그렇다고 해서 노력한 그룹과 그렇지 않은 그룹을 단순 비교하는 것은 "내가 노력하면 성공할 수 있어"라는 자기 암시와 믿음에서 이미 차이가 나기 때문에 적절한 비교가 아니다.
내가 성공한다는 믿음까지 온전히 통제해야 하는데 이를 관측해서 통제하는 것 역시 어려운 문제다. 관측하지 못하면 통제할 수 없고, 통제할 수 없으면 선택 편향이 생긴다.
내가 관측 가능한 요소에서 선택편향을 통제할 수 있으면 Selection on observables이라고 부른다. 그렇지 않은 경우를 Selection on unobservables이라고 하는데, 매칭/회귀분석은 Selection on observables 전략으로, 내가 관측하지 못하는 변수가 있다면 선택 편향이 계속 발생하게 된다는 한계가 있다.
매칭 방법론
매칭을 하기 위한 방법은 많다. 결국 어떤 식으로든 처치군(Treatment Group)과 대조군(Control Group)의 공변량이 비슷한 경우를 짝지어주면 되기 때문에 방법론도 다양하다. 이 글에서는 대표적인 몇 가지 방법에 대해서만 소개하려 한다.
PSM (Propensity Score Matching ; 성향점수매칭)
매칭의 가장 대표적인 방법이다. 처치 여부(Treatment)에 영향을 주는 변수들(Covariate)을 이용해서 먼저 처치 받을 확률(Propensity Score)을 구하고, 이러한 Propensity Score가 비슷한 경우만 매칭하여 비교한다는 개념이다. Propensity Score는 일반적으로 logistic regression을 사용해서 구한다.
가령 흡연이 당뇨에 미치는 영향을 분석한다고 하면, 흡연자와 비흡연자의 기본적인 건강 상태가 다를 수밖에 없다.
# R 의사코드
glm(흡연 ~ 성별 + 소득 + 연령 + 음주 + 교육, family = "binomial")
공변량을 통해 흡연할 가능성(logistic regression으로 구한 predict value)이 비슷한 그룹을 짝지어 매칭하는 것이 성향점수 매칭이다.
CEM(Coarsened Exact Matching)
앞의 PSM이 처치받을 확률이 비슷한 그룹끼리 매칭하는 개념이었다면, CEM은 좀 더 직관적으로 각 공변량의 구간을 나눠 그 구간에 들어오는 처치 그룹 / 통제 그룹끼리 비교하는 개념이다.
- 20대 / 30대 / 40대 ...
- 여자 / 남자
- 음주 월 1회 / 월 2회 / 월 3회 ...
- 대학원 졸 / 대학교 졸 / 고졸 / 중졸..
이렇게 각 변수의 구간을 나누고 그 구간에 해당하는 처치 / 통제그룹끼리 매칭하는 것이 CEM이다.
둘 중 어느 것을 써야하는지는 결정하기 어려운데 이는 각 방법론마다 장/단점이 있기 때문이다.
직관적으로 예를 들면 PSM은 언수외(라떼는 국수영이 아니었다 이말이야...) 점수의 합이 290점, 280점, 270점...인 학생들끼리 비교하는 전략이고 CEM은 언어 90 ~ 100점 / 수리 90 ~ 100점 / 외국어 90 ~ 100 점 범위에 다 들어온 학생들끼리만 비교하겠다는 전략이다.
언수외 합이 270점은 상대적으로 국어를 잘 하고, 수학을 못해도(언어 100점, 수리 70점, 외국어 100점) 나올 수 있고 과목을 골고루 잘 해도(언어 90 / 수리 90 / 외국어 90) 나올 수 있다. PSM 기준으로는 양쪽 다 언수외 270점을 만족하므로 매칭이 이렇게도 가능하다. 이러면 상대적으로 표본이 많아지는데, 대신 동일한 270점 학생끼리도 국어를 잘하는 학생 / 수학을 잘 하는 학생 / 영어를 잘 하는 학생이 만들어지므로, 즉 동일 그룹끼리도 과목별 점수 편차가 발생하여 분석에 어려움이 생길 수 있다.
반면 CEM은 각 과목별로 점수가 비슷한 사람끼리만 매칭하기 때문에 과목별 점수 편차가 나는 일은 없겠지만, 대신 표본이 줄어들기 때문에(소중한 샘플을 날림..) 분석에 어려움이 생길 수 있다.
실무에서 어떻게 썼는지
많이는 아니지만 매칭은 종종 실무에서 사용해 본 경험이 있다. (성공 / 실패 여부와는 별개로..) 위에서 말했던 Selection on observables이라는 한계 때문에 매칭을 통해 직접 인과 효과를 추정하는 경우는 거의 없었고, 뭔가 유저끼리 비교해야 하는 일이 올 때 선택 편향을 최대한 버리고 서로 비교 가능한 상태를 만들기 위해 사용했었다.
매칭 -----------> 인과효과 분석 이 단계에서 매칭까지는 그대로 진행하고, 이후 분석은 EDA로만 진행했는데, 이를 통해 스스로 EDA에 대한 자신감을 얻을 수 있는 효과가 있었다(?)
실제 매칭을 통해 인과 효과를 추정하기 위해서는 이 정도면 내가 관측 가능한 변수로 Selection Bias를 충분히 통제했다는 도메인 지식과 자신감이 중요할 것 같다.
R 실습 코드
이제 R로도 실습해보자! R에 대한 수요가 많이 없을 것 같기는 하지만... 통계 분석을 하는 건 파이썬보다 R이 압도적으로 코드 길이도 짧고, 전처리 단계가 줄어 편하다는 이점이 있다. (더불어 내가 R 유저라 R 코드가 편한 영향도 있다.)
파이썬에 대해서도 코드와 필요한 라이브러리에 대해 짧게 후술하려 한다.
데이터셋
분석에 사용할 데이터는 MatchIt 라이브러리 내에 내장된 lalonde 데이터를 사용하려고 한다.
해당 데이터는 PSM을 평가하기 위해 만들어진 데이터 셋이라고 하는데, 매칭을 적용해보기에 깔끔하게 떨어진다는 뜻이기도 하다.
해당 데이터는 직업교육 훈련(`treat` 변수)이 78년도 소득(`re78` 변수)에 어떤 영향을 미쳤는지를 분석하기 위한 데이터로, 직업 교육이라는 처치 변수 이외에 공변량으로 쓸 수 있는 변수는 나이(age), 교육연수(education), race(인종 : 흑인 / 백인 / 히스패닉으로 구성), 결혼 여부(married), nodegree (고등학교 학위여부, 1인 경우가 고등학교 학위가 없음), re74, re75(각각 74, 75년도 소득)로 구성되어 있다.
데이터 로드 및 EDA
rm(list = ls())
# 라이브러리 로드
library(tidyverse)
library(MatchIt)
library(GGally)
# install.packages("cobalt")
library(cobalt)
# 데이터 불러오기 ====
data("lalonde")
str(lalonde)
lalonde_trans <- lalonde
lalonde_trans$treat <- as.factor(lalonde_trans$treat)
lalonde_trans$married <- as.factor(lalonde_trans$married)
lalonde_trans$nodegree <- as.factor(lalonde_trans$nodegree)
# EDA ====
# ggpairs(lalonde_trans)
# 직업교육 참여 여부에 따른 인종 구성비
ggplot(data = lalonde_trans, aes(x=race, fill=treat)) + geom_bar() + facet_wrap(.~treat) + theme_bw()
# 직업교육 참여 여부에 따른 결혼 여부 구성비
ggplot(data = lalonde_trans, aes(x=married, fill=treat)) + geom_bar() + facet_wrap(.~treat) + theme_bw()
# 직업교육 참여 여부에 따른 학위 상태 구성비
ggplot(data = lalonde_trans, aes(x=nodegree, fill=treat)) + geom_bar() + facet_wrap(.~treat) + theme_bw()
# 직업교육 참여여부 별로 교육연수 차이가 있었는지
ggplot(data = lalonde_trans, aes(x=treat, y=educ)) + geom_boxplot()
# 직업교육 참여여부 이전 74년 소득이 어땠는지
ggplot(data = lalonde_trans, aes(x=treat, y=re74)) + geom_boxplot()
필수 라이브러리를 로드해주고, 데이터도 불러와 준다. 일부 변수에 대해서는 factor(범주형 변수)로 형 변환을 해줬다.
GGally의 ggpair 함수를 쓰면 데이터 셋에 대해 한 번에 EDA를 해주지만, 보기가 힘들어서 ggplot을 써서 EDA를 다시 해줬다.
아래 시각화 결과에서 0인 쪽이 직업교육 미참여, 1인 쪽이 직업 교육을 참여한 그룹이다.
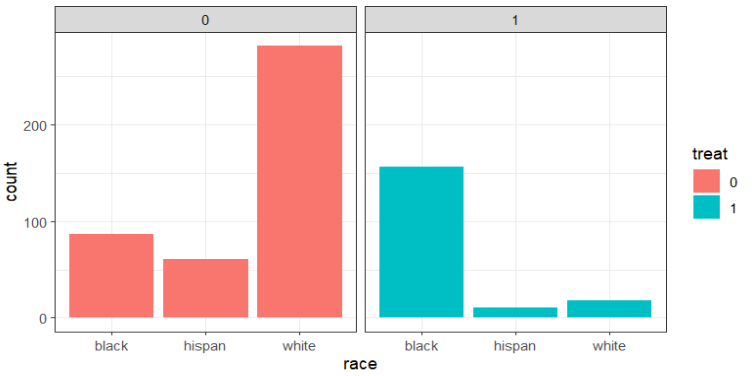
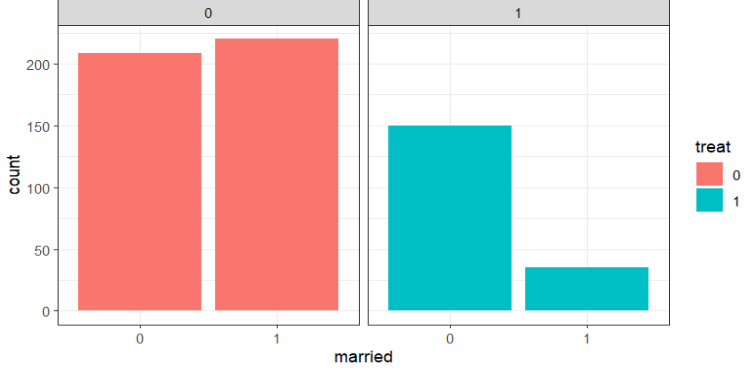
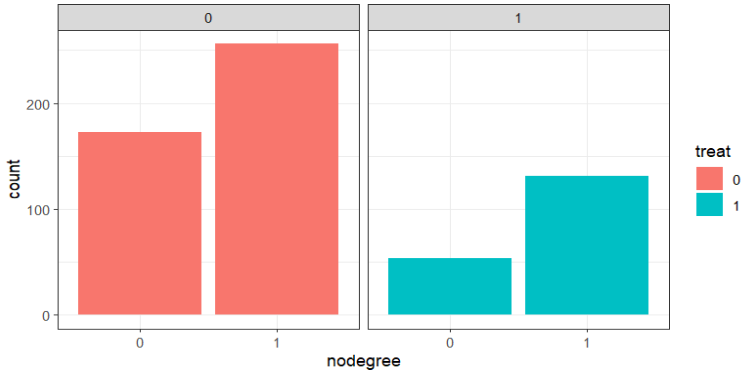
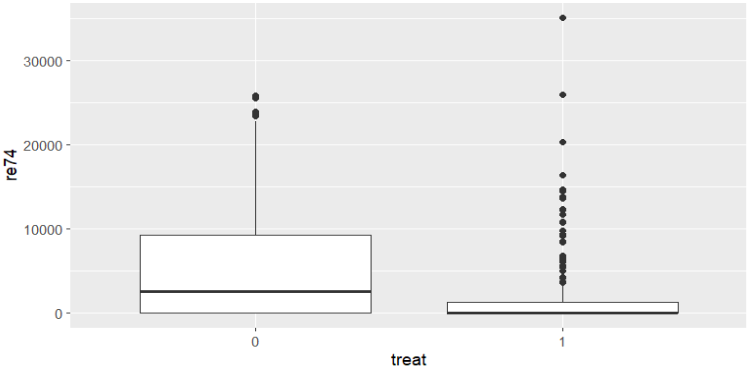
대충 봐도 직업교육에 참여한 그룹과 그렇지 않은 그룹 간 특징이 다르다..
매칭
이제 매칭을 통해 불균형을 최대한 없애보자! 먼저 PSM을 적용해보자.
psm <- matchit(data = lalonde_trans,
treat ~ age + educ + race + married + nodegree + re74 + re75,
method = "nearest", distance = "glm")
summary(psm)
MatchIt 라이브러리에 내장된 matchit 함수를 쓰면 매칭을 쉽게 할 수 있다. method라는 인자와 distance라는 인자를 받아올 수 있는데, method라는 인자에 대해 ChatGPT에 물어보니 상세한 답을 얻을 수 있었다.

"nearest" 옵션이나 "optimal"을 PSM 을 구할 때 고려해봄직 하다.
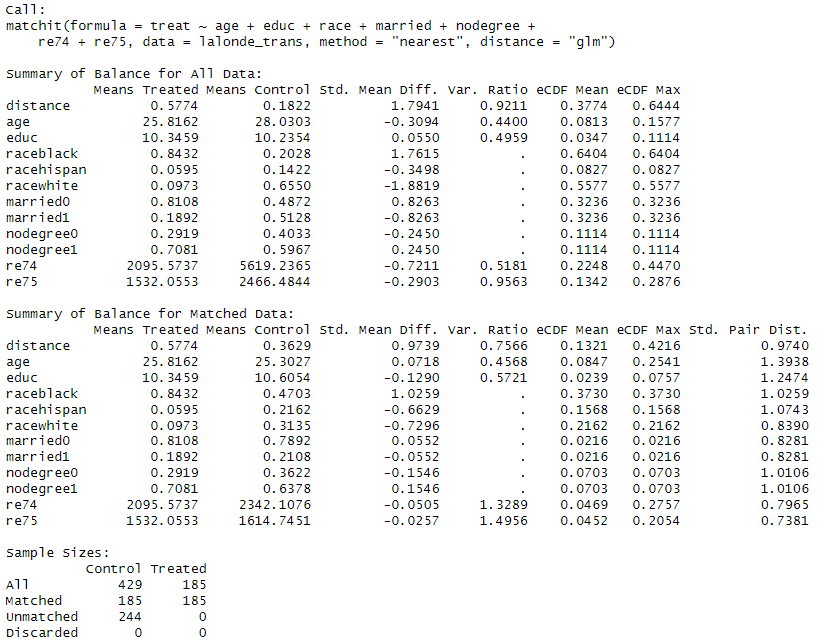
수많은 문자와 숫자의 향연이라 알아보기는 어렵지만, Summary of Balance라고 쓰여 있는 제목을 중심으로 해석하면 된다. 처음 나온 Summary of Balance for All Data는 매칭 전의 Treatment 그룹과 Control 그룹의 공변량의 특성을 비교한 것이다. 앞서 EDA에서 본 것처럼 특성이 다르다.
그러면 Matching을 마친 Summary of Balance for Matched Data의 결과는 어떨까?
인종 구성이 여전히 다르다. 교육 연수 차이는 오히려 더 벌어진 것 같다. PSM을 바로 적용하자니 뭔가 찝집하다. 그러면 CEM도 적용해보자.
cem <- matchit(data=lalonde_trans,
treat ~ age + educ + race + married + nodegree + re74 + re75,
method = "cem", distance = "glm")
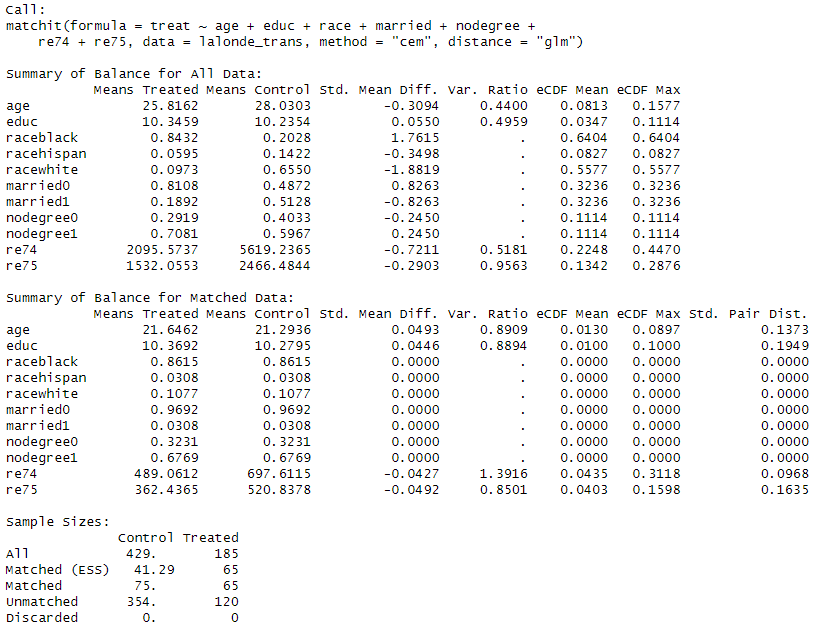
아까보다 공변량의 밸런스가 잘 맞는 것 같다.
매칭 후 공변량의 밸런스 상태는 cobalt라는 라이브러리로도 확인할 수 있다.
library(cobalt)
love.plot(cem)
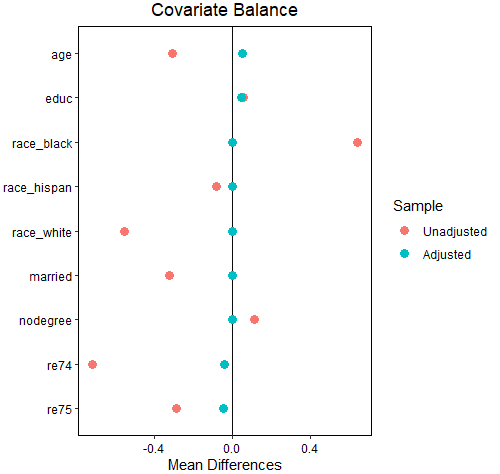
단 한 줄의 코드면 된다. 물론 세부적인 파라미터를 지정해서 볼 수 있기는 하지만, 인자를 따로지정해주지 않아도 love.plot이라는 함수에 앞서 매칭을 돌렸던 모형 변수명을 넣어주면 SMD(Standardized Mean Differences, 그룹의 평균 차이를 그룹 간 표준편차의 가중평균으로 나눠준 값)을 자동으로 비교한다. 당연히 양쪽 그룹의 차이가 없어야 이상적이므로 매칭이 잘 되었다면 SMD는 0에 가까워야 한다.
빨간 점이 매칭 전, 파란 점이 매칭 후인데 대부분 CEM으로 매칭한 이후, SMD가 0에 가까워졌다.
CEM을 적용하여 비슷한 공변량의 특성을 가진 데이터를 얻으려면 match.data 함수를 써주면 된다. 그러면 원래 raw data보다 줄어든 레코드와 늘어난 컬럼이 나온다.
cem.out <- match.data(cem)
# 인과효과 분석 ====
casual <- lm(data = cem.out, re78 ~ treat + age + educ + race + married + nodegree + re74 + re75)
summary(casual)
이제 인과효과 분석을 해보자. 조금 러프하다면 러프하고, 무식하다면 무식한 방법이지만 선택편향을 덜어낸 데이터 통째로 회귀분석을 돌려본다.
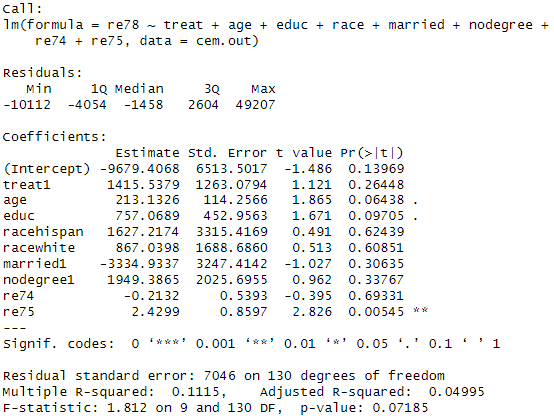
우리의 관심사는 treat1 변수로, 직업 훈련 참여 여부가 소득에 유의미한 영향을 미치는지를 보고 싶었기 때문에 다른 공변량의 효과는 무시하고, treat1의 p value를 보면 된다. 그 결과 0.26의 p value로 유의하지 않다고 나온다..
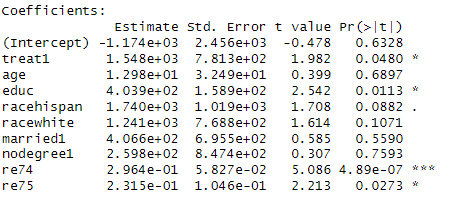
매칭을 하지 않은 상태로(최초 raw data 사용) 회귀분석을 돌리면 아래 결과가 나오는데, 이는 직업 훈련이 소득 증가에 유의한 영향을 미쳤다는 결론이 나온다. 즉, 매칭을 했는지, 하지 않았는지에 따라 인과 해석이 완전히 달라져 버린다.
Sensitivity Test
Sensitivity Test로 분석 과정을 마무리해보려 한다. Sensitivity Test에 대해서는 잘 알지는 못해서 library를 간략하게 소개하는 정도로만 정리할 예정이다.
먼저 Sensitivity Test는 만일 처치변수와 결과변수에 동시에 영향을 미치지만 관측하지 못한 가상의 변수(unobserved factor)가 있다면 이 변수가 Treatment가 Outcome에 미치는 영향을 얼마나 달라지게 만드는지 확인하는 방법이다.
이를 위한 여러 라이브러리가 있지만 여기서는 'sensemakr'라는 라이브러리를 써보려고 한다.
library(sensemakr)
sensitivity_analysis <- sensemakr(casual, treatment = "treat1",
benchmark_covariates = c("age", "educ","re74", "re75", "racehispan",
"racewhite", "married1", "nodegree1")
)
summary(sensitivity_analysis)
앞서 매칭 데이터로 회귀분석을 돌렸던 모델을 parameter로 넣어준다 (causal이라는 변수명)
그 다음에 treatment에는 처치 변수가 될 변수명을 넣어준다. treat로 넣으니 동작이 안 되었는데, 아마 treat가 범주형이라 안 되는 것 같다. 회귀계수가 붙은 treat1로 변수명을 바꿔주니 동작을 했다.
benchmark_covariates에는 공변량의 목록을 작성해서 넣어준다. 관측되지 않은 가상의 공변량을 만들 때 benchmark_covariates에 있는 변수들을 참조해서 가상의 공변량의 bound를 정하는데 쓰인다.
summary로 결과를 요약하면 꽤나 긴 문장이 나오는데, 이 중 Partial R2 of the treatment with the outcome에 대해서만 간략히 설명하려 한다.
만약 관찰되지 않은 변수가 결과 변수(outcome)에 100%로 영향을 미친다고 가정해보자. 만일 unobserved factor가 처치 변수(Treatment variable)에도 동시에 영향을 미친다면, unobserved factor는 treatment와도 상관관계를 갖게 되어, Treatment에도 어느 정도의 설명력을 갖게 된다. 이 설명력이 작으면 작을수록 좋은데, 이에 해당하는 내용이 Partial R2 of the treatment with the outcome다.
Python 실습을 위한 라이브러리 안내
파이썬에서도 위와 같은 일련의 과정을 지원하는 라이브러리가 당연히 있다.
- PSM을 구할 때 쓰는 statsmodels
- nearest 매칭을 구하도록 도와주는 causalml
- CEM 매칭에 사용할 수 있는 cem
- 그리고 sensitivity test는 Pysensemakr를 쓸 수 있는데,
R보다는 파이썬 쪽이 패키지 호환성을 맞추기가 어렵다보니, 코드를 상세하게 작성하기가 어려웠다.
대략 느낌만 볼 수 있도록 위와 같은 데이터셋이 동일하게 있다고 가정하고, PSM을 구하는 과정만 작성해보려 한다.
import causalml
import pandas as pd
import numpy as np
from causalml.match import NearestNeighborMatch
import statsmodels.api as sm
# 범주형 변수를 원핫 인코딩
lalonde = pd.get_dummies(lalonde)
# PS(Propensity score)를 구하기 위한 데이터 전처리
Treat = lalonde['treat']
Outcome = lalonde['re78']
feature = lalonde.drop(labels = ['treat', 're78'], axis = 1)
feature = feature.astype(
{'race_black':'int64', 'race_hispan':'int64', 'race_white':'int64'}
)
# PS(Propensity score) 계산
feature_new = sm.add_constant(feature)
ps = sm.Logit(Treat, feature_new).fit()
# 구한 PS를 기준으로 매칭
lalonde['propensity_score'] = ps.predict(feature_new)
nnm = causalml.match.NearestNeighborMatch(replace=False, ratio=1, random_state=42)
matched = nnm.match(data=lalonde, treatment_col='treat', score_cols=['propensity_score'])
# 매칭 결과를 기준으로 인과추론
from statsmodels.formula.api import ols
model = ols(formula = 're78 ~ treat + age + educ + married + nodegree + re74 + re75 + race_black + race_hispan + race_white',
data = matched).fit()
print(model.summary())
꽤나 긴 글이었는데 어느덧 끝이 보인다. 누군가에게도 이 글이 도움이 되길 바라며 마무리 해본다.

'Statistics' 카테고리의 다른 글
| 인과추론 학습기 - SCM과 인과 그래프 (3) | 2024.10.19 |
|---|---|
| 인과추론을 위한 회귀분석 개념 정리 - 편회귀계수, FWL 정리 (2) | 2024.04.21 |
| 꼬리에 꼬리를 무는 시계열 개념 정리, 정상성부터 공적분까지 (4) | 2024.01.14 |
| 인과추론 학습기 - 회귀 불연속(Regression Discontinuity) (0) | 2023.08.25 |
| 베이즈 통계학을 공부하면 좋은 이유 (1) | 2023.07.29 |
배경
최근 매칭을 업무에 오랜만에 써보는 일이 있었다. 오랜만에 써봐서 잊고 있었는데 매칭은 은근 분석에 도움이 되어, 가끔씩이라도 쓰게 되는 일이 있는 것 같다는 생각이 들었다. 향후 다시 매칭을 써먹을 나를 위해, 그리고 매칭을 적용해보고 싶은 사람들을 위해 정리할 겸 글을 남기게 되었다.
글은 매칭의 개념, 매칭의 한계, 매칭 방법에 대한 간단한 소개, 매칭에 사용하는 코드(R 위주) 순으로 진행하려 한다.

매칭의 개념 및 목적
매칭은 간단히 말하면 Treatment 그룹(처치군 ; 처치를 받은 대상)과 Control 그룹(대조군 ; 처치를 받지 않은 대상) 간 특성이 비슷한 사람을 짝지어주는 것을 의미한다.
이러한 짝짓기가 필요한 이유는 Selection Bias(선택 편향) 때문인데, 선택 편향의 정의를 살펴보면 다음과 같다.
선택 편향(영어: selection bias) 또는 선택적 보고(영어: selective reporting)는 표본을 사전 또는 사후 선택함에 따라 통계 분석을 왜곡하는 오류다. 일반적으로 이것은 통계적 유의성의 척도를 실제보다 더 크게 나타나도록 만든다.
출처 : 위키백과
예를 들어 선택 편향을 고려하지 않으면 병원에 입원한 사람이 그렇지 않은 사람보다 건강 정도가 더 나쁘기 때문에 병원 입원이 건강 악화를 야기한다는 잘못된 결과를 낼 수 있다. 병원에 입원하는 사람은 건강이 매우 나빠졌기 때문에 입원하는 경우가 일반적이므로, 단순히 입원한 사람과 그렇지 않은 사람을 비교하는 것은 올바르지 않다는 의미이다.
매칭의 전략은 Covariate(공변량)이 비슷한 사람끼리 짝짓고, 비슷한 사람까리만 Outcome variable(우리가 보려고 하는 성과변수, 위의 예시에서는 건강 상태)를 비교하여 Selection Bias를 줄이려고 하는 것이다. 위의 예시 기준으로는 성별 / 흡연 여부 / 음주 여부 / 주 운동 횟수 / 이전 병력 등이 비슷한 사람 중에 병원 입원을 택한 그룹(Treatment)과 방문 진료를 택한 그룹(Control)의 진료 이후의 건강 상태를 비교해야만 올바른 비교가 될 수 있는 뜻이다.

회귀분석과의 공통점/차이점
공변량(Covariate)이 비슷한 사람끼리 짝짓는다는 점에서 매칭은 회귀분석(Regression)과 비교가 가능하다. 회귀분석 역시 성과변수(Outcome Variable)에 영향을 미치는 요인으로 처치변수(Treatment Variable)과 공변량(Covariate)를 같이 활용할 수 있다. 다시 말해 공변량(Covariate)이 통제된 상태에서 처치 효과(Treatment Effect)를 비교한다는 측면에서 매칭과 회귀분석은 공통점을 갖고 있다.
대체로 해롭지 않은 경제학에서는 회귀분석 역시 특수한 형태의 매칭이라고 언급하기도 하는데, 이는 회귀분석 역시 매칭의 한 범주에 들어갈 수 있음을 의미한다.
그렇지만 회귀분석과 매칭은 차이가 있다. 먼저 처치효과(Treatment Effect)를 구하는 방식에 차이가 있다. 매칭의 경우, 처치(Treatment)를 받을 가능성이 높은 공변량(Covariate)에 더 큰 가중치를 부여한다. 그렇지만 회귀분석은 \(Cov(X,\tilde{D})/Var(\tilde{D})\) 이 큰 쪽, 즉 조건부 분산이 더 큰 가중치를 부여한다.
회귀분석은 회귀식(Functional Form)에 크게 의존한다. 회귀 식에 변수 간 상호작용(interaction)을 고려할 것인지, N차항을 고려할 것인지에 따라 처치효과(Treatment Effect)가 달라지게 된다. 반면 매칭은 꼭 회귀식의 형태가 아니더라도 처치그룹(Treatment)과 대조군(Control)을 비교할 수 있다. 즉, Functional Form에 대한 의존도가 회귀분석보다는 낮은 편이다.
매칭의 한계점
매칭도, 회귀분석도 모두 공통적인 한계가 있다. 공변량(Covariate)을 통제해서 선택 편향(Selection Bias)을 제거하는 전략은 통제해야 할 공변량을 빼먹게 된다면 여전히 선택 편향이 남아버리는 맹점이 있다.
"노력하면 성공한다"라는 문장을 인과적으로 분석한다고 가정해보자. 일단 "노력"과 "성공"이라는 걸 정량화할 수 있는지는 차치하더라도, 그래서 나름대로 노력과 성공을 정량화할 수 있는 기준을 찾아내더라도 "노력하는 사람"과 "노력하지 않는 사람"을 온전히 비교하기는 어렵다.


"노력"이라는 것도 타고난 유전이나 재능이라고 이야기하는 경우를 꽤 많이 봤다. 논의가 거기에만 그치면 다행이지만, 정말 슬프게도 내가 노력하지 않는 건 노력이라는 재능을 타고나지 못했다고 아예 시도도 하지 않고 손을 놔버리는 경우가 있다고도 들었다.

굳이 뭔가 분석하지 않아도, 상식적으로는 노력하는 쪽이 노력하지 않은 쪽보다 더 성공할 확률이 높을 것이다. 그렇다고 해서 노력한 그룹과 그렇지 않은 그룹을 단순 비교하는 것은 "내가 노력하면 성공할 수 있어"라는 자기 암시와 믿음에서 이미 차이가 나기 때문에 적절한 비교가 아니다.
내가 성공한다는 믿음까지 온전히 통제해야 하는데 이를 관측해서 통제하는 것 역시 어려운 문제다. 관측하지 못하면 통제할 수 없고, 통제할 수 없으면 선택 편향이 생긴다.
내가 관측 가능한 요소에서 선택편향을 통제할 수 있으면 Selection on observables이라고 부른다. 그렇지 않은 경우를 Selection on unobservables이라고 하는데, 매칭/회귀분석은 Selection on observables 전략으로, 내가 관측하지 못하는 변수가 있다면 선택 편향이 계속 발생하게 된다는 한계가 있다.
매칭 방법론
매칭을 하기 위한 방법은 많다. 결국 어떤 식으로든 처치군(Treatment Group)과 대조군(Control Group)의 공변량이 비슷한 경우를 짝지어주면 되기 때문에 방법론도 다양하다. 이 글에서는 대표적인 몇 가지 방법에 대해서만 소개하려 한다.
PSM (Propensity Score Matching ; 성향점수매칭)
매칭의 가장 대표적인 방법이다. 처치 여부(Treatment)에 영향을 주는 변수들(Covariate)을 이용해서 먼저 처치 받을 확률(Propensity Score)을 구하고, 이러한 Propensity Score가 비슷한 경우만 매칭하여 비교한다는 개념이다. Propensity Score는 일반적으로 logistic regression을 사용해서 구한다.
가령 흡연이 당뇨에 미치는 영향을 분석한다고 하면, 흡연자와 비흡연자의 기본적인 건강 상태가 다를 수밖에 없다.
# R 의사코드
glm(흡연 ~ 성별 + 소득 + 연령 + 음주 + 교육, family = "binomial")
공변량을 통해 흡연할 가능성(logistic regression으로 구한 predict value)이 비슷한 그룹을 짝지어 매칭하는 것이 성향점수 매칭이다.
CEM(Coarsened Exact Matching)
앞의 PSM이 처치받을 확률이 비슷한 그룹끼리 매칭하는 개념이었다면, CEM은 좀 더 직관적으로 각 공변량의 구간을 나눠 그 구간에 들어오는 처치 그룹 / 통제 그룹끼리 비교하는 개념이다.
- 20대 / 30대 / 40대 ...
- 여자 / 남자
- 음주 월 1회 / 월 2회 / 월 3회 ...
- 대학원 졸 / 대학교 졸 / 고졸 / 중졸..
이렇게 각 변수의 구간을 나누고 그 구간에 해당하는 처치 / 통제그룹끼리 매칭하는 것이 CEM이다.
둘 중 어느 것을 써야하는지는 결정하기 어려운데 이는 각 방법론마다 장/단점이 있기 때문이다.
직관적으로 예를 들면 PSM은 언수외(라떼는 국수영이 아니었다 이말이야...) 점수의 합이 290점, 280점, 270점...인 학생들끼리 비교하는 전략이고 CEM은 언어 90 ~ 100점 / 수리 90 ~ 100점 / 외국어 90 ~ 100 점 범위에 다 들어온 학생들끼리만 비교하겠다는 전략이다.
언수외 합이 270점은 상대적으로 국어를 잘 하고, 수학을 못해도(언어 100점, 수리 70점, 외국어 100점) 나올 수 있고 과목을 골고루 잘 해도(언어 90 / 수리 90 / 외국어 90) 나올 수 있다. PSM 기준으로는 양쪽 다 언수외 270점을 만족하므로 매칭이 이렇게도 가능하다. 이러면 상대적으로 표본이 많아지는데, 대신 동일한 270점 학생끼리도 국어를 잘하는 학생 / 수학을 잘 하는 학생 / 영어를 잘 하는 학생이 만들어지므로, 즉 동일 그룹끼리도 과목별 점수 편차가 발생하여 분석에 어려움이 생길 수 있다.
반면 CEM은 각 과목별로 점수가 비슷한 사람끼리만 매칭하기 때문에 과목별 점수 편차가 나는 일은 없겠지만, 대신 표본이 줄어들기 때문에(소중한 샘플을 날림..) 분석에 어려움이 생길 수 있다.
실무에서 어떻게 썼는지
많이는 아니지만 매칭은 종종 실무에서 사용해 본 경험이 있다. (성공 / 실패 여부와는 별개로..) 위에서 말했던 Selection on observables이라는 한계 때문에 매칭을 통해 직접 인과 효과를 추정하는 경우는 거의 없었고, 뭔가 유저끼리 비교해야 하는 일이 올 때 선택 편향을 최대한 버리고 서로 비교 가능한 상태를 만들기 위해 사용했었다.
매칭 -----------> 인과효과 분석 이 단계에서 매칭까지는 그대로 진행하고, 이후 분석은 EDA로만 진행했는데, 이를 통해 스스로 EDA에 대한 자신감을 얻을 수 있는 효과가 있었다(?)
실제 매칭을 통해 인과 효과를 추정하기 위해서는 이 정도면 내가 관측 가능한 변수로 Selection Bias를 충분히 통제했다는 도메인 지식과 자신감이 중요할 것 같다.
R 실습 코드
이제 R로도 실습해보자! R에 대한 수요가 많이 없을 것 같기는 하지만... 통계 분석을 하는 건 파이썬보다 R이 압도적으로 코드 길이도 짧고, 전처리 단계가 줄어 편하다는 이점이 있다. (더불어 내가 R 유저라 R 코드가 편한 영향도 있다.)
파이썬에 대해서도 코드와 필요한 라이브러리에 대해 짧게 후술하려 한다.
데이터셋
분석에 사용할 데이터는 MatchIt 라이브러리 내에 내장된 lalonde 데이터를 사용하려고 한다.
해당 데이터는 PSM을 평가하기 위해 만들어진 데이터 셋이라고 하는데, 매칭을 적용해보기에 깔끔하게 떨어진다는 뜻이기도 하다.
해당 데이터는 직업교육 훈련(`treat` 변수)이 78년도 소득(`re78` 변수)에 어떤 영향을 미쳤는지를 분석하기 위한 데이터로, 직업 교육이라는 처치 변수 이외에 공변량으로 쓸 수 있는 변수는 나이(age), 교육연수(education), race(인종 : 흑인 / 백인 / 히스패닉으로 구성), 결혼 여부(married), nodegree (고등학교 학위여부, 1인 경우가 고등학교 학위가 없음), re74, re75(각각 74, 75년도 소득)로 구성되어 있다.
데이터 로드 및 EDA
rm(list = ls())
# 라이브러리 로드
library(tidyverse)
library(MatchIt)
library(GGally)
# install.packages("cobalt")
library(cobalt)
# 데이터 불러오기 ====
data("lalonde")
str(lalonde)
lalonde_trans <- lalonde
lalonde_trans$treat <- as.factor(lalonde_trans$treat)
lalonde_trans$married <- as.factor(lalonde_trans$married)
lalonde_trans$nodegree <- as.factor(lalonde_trans$nodegree)
# EDA ====
# ggpairs(lalonde_trans)
# 직업교육 참여 여부에 따른 인종 구성비
ggplot(data = lalonde_trans, aes(x=race, fill=treat)) + geom_bar() + facet_wrap(.~treat) + theme_bw()
# 직업교육 참여 여부에 따른 결혼 여부 구성비
ggplot(data = lalonde_trans, aes(x=married, fill=treat)) + geom_bar() + facet_wrap(.~treat) + theme_bw()
# 직업교육 참여 여부에 따른 학위 상태 구성비
ggplot(data = lalonde_trans, aes(x=nodegree, fill=treat)) + geom_bar() + facet_wrap(.~treat) + theme_bw()
# 직업교육 참여여부 별로 교육연수 차이가 있었는지
ggplot(data = lalonde_trans, aes(x=treat, y=educ)) + geom_boxplot()
# 직업교육 참여여부 이전 74년 소득이 어땠는지
ggplot(data = lalonde_trans, aes(x=treat, y=re74)) + geom_boxplot()
필수 라이브러리를 로드해주고, 데이터도 불러와 준다. 일부 변수에 대해서는 factor(범주형 변수)로 형 변환을 해줬다.
GGally의 ggpair 함수를 쓰면 데이터 셋에 대해 한 번에 EDA를 해주지만, 보기가 힘들어서 ggplot을 써서 EDA를 다시 해줬다.
아래 시각화 결과에서 0인 쪽이 직업교육 미참여, 1인 쪽이 직업 교육을 참여한 그룹이다.




대충 봐도 직업교육에 참여한 그룹과 그렇지 않은 그룹 간 특징이 다르다..
매칭
이제 매칭을 통해 불균형을 최대한 없애보자! 먼저 PSM을 적용해보자.
psm <- matchit(data = lalonde_trans,
treat ~ age + educ + race + married + nodegree + re74 + re75,
method = "nearest", distance = "glm")
summary(psm)
MatchIt 라이브러리에 내장된 matchit 함수를 쓰면 매칭을 쉽게 할 수 있다. method라는 인자와 distance라는 인자를 받아올 수 있는데, method라는 인자에 대해 ChatGPT에 물어보니 상세한 답을 얻을 수 있었다.

"nearest" 옵션이나 "optimal"을 PSM 을 구할 때 고려해봄직 하다.

수많은 문자와 숫자의 향연이라 알아보기는 어렵지만, Summary of Balance라고 쓰여 있는 제목을 중심으로 해석하면 된다. 처음 나온 Summary of Balance for All Data는 매칭 전의 Treatment 그룹과 Control 그룹의 공변량의 특성을 비교한 것이다. 앞서 EDA에서 본 것처럼 특성이 다르다.
그러면 Matching을 마친 Summary of Balance for Matched Data의 결과는 어떨까?
인종 구성이 여전히 다르다. 교육 연수 차이는 오히려 더 벌어진 것 같다. PSM을 바로 적용하자니 뭔가 찝집하다. 그러면 CEM도 적용해보자.
cem <- matchit(data=lalonde_trans,
treat ~ age + educ + race + married + nodegree + re74 + re75,
method = "cem", distance = "glm")

아까보다 공변량의 밸런스가 잘 맞는 것 같다.
매칭 후 공변량의 밸런스 상태는 cobalt라는 라이브러리로도 확인할 수 있다.
library(cobalt)
love.plot(cem)
단 한 줄의 코드면 된다. 물론 세부적인 파라미터를 지정해서 볼 수 있기는 하지만, 인자를 따로지정해주지 않아도 love.plot이라는 함수에 앞서 매칭을 돌렸던 모형 변수명을 넣어주면 SMD(Standardized Mean Differences, 그룹의 평균 차이를 그룹 간 표준편차의 가중평균으로 나눠준 값)을 자동으로 비교한다. 당연히 양쪽 그룹의 차이가 없어야 이상적이므로 매칭이 잘 되었다면 SMD는 0에 가까워야 한다.
빨간 점이 매칭 전, 파란 점이 매칭 후인데 대부분 CEM으로 매칭한 이후, SMD가 0에 가까워졌다.

CEM을 적용하여 비슷한 공변량의 특성을 가진 데이터를 얻으려면 match.data 함수를 써주면 된다. 그러면 원래 raw data보다 줄어든 레코드와 늘어난 컬럼이 나온다.
cem.out <- match.data(cem)
# 인과효과 분석 ====
casual <- lm(data = cem.out, re78 ~ treat + age + educ + race + married + nodegree + re74 + re75)
summary(casual)
이제 인과효과 분석을 해보자. 조금 러프하다면 러프하고, 무식하다면 무식한 방법이지만 선택편향을 덜어낸 데이터 통째로 회귀분석을 돌려본다.

우리의 관심사는 treat1 변수로, 직업 훈련 참여 여부가 소득에 유의미한 영향을 미치는지를 보고 싶었기 때문에 다른 공변량의 효과는 무시하고, treat1의 p value를 보면 된다. 그 결과 0.26의 p value로 유의하지 않다고 나온다..
매칭을 하지 않은 상태로(최초 raw data 사용) 회귀분석을 돌리면 아래 결과가 나오는데, 이는 직업 훈련이 소득 증가에 유의한 영향을 미쳤다는 결론이 나온다. 즉, 매칭을 했는지, 하지 않았는지에 따라 인과 해석이 완전히 달라져 버린다.

Sensitivity Test
Sensitivity Test로 분석 과정을 마무리해보려 한다. Sensitivity Test에 대해서는 잘 알지는 못해서 library를 간략하게 소개하는 정도로만 정리할 예정이다.
먼저 Sensitivity Test는 만일 처치변수와 결과변수에 동시에 영향을 미치지만 관측하지 못한 가상의 변수(unobserved factor)가 있다면 이 변수가 Treatment가 Outcome에 미치는 영향을 얼마나 달라지게 만드는지 확인하는 방법이다.
이를 위한 여러 라이브러리가 있지만 여기서는 'sensemakr'라는 라이브러리를 써보려고 한다.
library(sensemakr)
sensitivity_analysis <- sensemakr(casual, treatment = "treat1",
benchmark_covariates = c("age", "educ","re74", "re75", "racehispan",
"racewhite", "married1", "nodegree1")
)
summary(sensitivity_analysis)
앞서 매칭 데이터로 회귀분석을 돌렸던 모델을 parameter로 넣어준다 (causal이라는 변수명)
그 다음에 treatment에는 처치 변수가 될 변수명을 넣어준다. treat로 넣으니 동작이 안 되었는데, 아마 treat가 범주형이라 안 되는 것 같다. 회귀계수가 붙은 treat1로 변수명을 바꿔주니 동작을 했다.
benchmark_covariates에는 공변량의 목록을 작성해서 넣어준다. 관측되지 않은 가상의 공변량을 만들 때 benchmark_covariates에 있는 변수들을 참조해서 가상의 공변량의 bound를 정하는데 쓰인다.
summary로 결과를 요약하면 꽤나 긴 문장이 나오는데, 이 중 Partial R2 of the treatment with the outcome에 대해서만 간략히 설명하려 한다.
만약 관찰되지 않은 변수가 결과 변수(outcome)에 100%로 영향을 미친다고 가정해보자. 만일 unobserved factor가 처치 변수(Treatment variable)에도 동시에 영향을 미친다면, unobserved factor는 treatment와도 상관관계를 갖게 되어, Treatment에도 어느 정도의 설명력을 갖게 된다. 이 설명력이 작으면 작을수록 좋은데, 이에 해당하는 내용이 Partial R2 of the treatment with the outcome다.
Python 실습을 위한 라이브러리 안내
파이썬에서도 위와 같은 일련의 과정을 지원하는 라이브러리가 당연히 있다.
- PSM을 구할 때 쓰는 statsmodels
- nearest 매칭을 구하도록 도와주는 causalml
- CEM 매칭에 사용할 수 있는 cem
- 그리고 sensitivity test는 Pysensemakr를 쓸 수 있는데,
R보다는 파이썬 쪽이 패키지 호환성을 맞추기가 어렵다보니, 코드를 상세하게 작성하기가 어려웠다.
대략 느낌만 볼 수 있도록 위와 같은 데이터셋이 동일하게 있다고 가정하고, PSM을 구하는 과정만 작성해보려 한다.
import causalml
import pandas as pd
import numpy as np
from causalml.match import NearestNeighborMatch
import statsmodels.api as sm
# 범주형 변수를 원핫 인코딩
lalonde = pd.get_dummies(lalonde)
# PS(Propensity score)를 구하기 위한 데이터 전처리
Treat = lalonde['treat']
Outcome = lalonde['re78']
feature = lalonde.drop(labels = ['treat', 're78'], axis = 1)
feature = feature.astype(
{'race_black':'int64', 'race_hispan':'int64', 'race_white':'int64'}
)
# PS(Propensity score) 계산
feature_new = sm.add_constant(feature)
ps = sm.Logit(Treat, feature_new).fit()
# 구한 PS를 기준으로 매칭
lalonde['propensity_score'] = ps.predict(feature_new)
nnm = causalml.match.NearestNeighborMatch(replace=False, ratio=1, random_state=42)
matched = nnm.match(data=lalonde, treatment_col='treat', score_cols=['propensity_score'])
# 매칭 결과를 기준으로 인과추론
from statsmodels.formula.api import ols
model = ols(formula = 're78 ~ treat + age + educ + married + nodegree + re74 + re75 + race_black + race_hispan + race_white',
data = matched).fit()
print(model.summary())
꽤나 긴 글이었는데 어느덧 끝이 보인다. 누군가에게도 이 글이 도움이 되길 바라며 마무리 해본다.

'Statistics' 카테고리의 다른 글
| 인과추론 학습기 - SCM과 인과 그래프 (3) | 2024.10.19 |
|---|---|
| 인과추론을 위한 회귀분석 개념 정리 - 편회귀계수, FWL 정리 (2) | 2024.04.21 |
| 꼬리에 꼬리를 무는 시계열 개념 정리, 정상성부터 공적분까지 (4) | 2024.01.14 |
| 인과추론 학습기 - 회귀 불연속(Regression Discontinuity) (0) | 2023.08.25 |
| 베이즈 통계학을 공부하면 좋은 이유 (1) | 2023.07.29 |
