오늘은 개입(intervention)과 뒷문기준(frontdoor criterion)에 대한 글을 써보려고 한다.
이를 이해하기 위해서는 인과 그래프에 대한 선행지식이 필요하다.
https://blessedby-clt.tistory.com/78
인과추론 학습기 - SCM과 인과 그래프
오늘은 인과추론의 주요 개념 중 하나인 인과 그래프에 대한 글을 써보려고 한다.독립, 조건부 독립 등 기초 통계회귀분석에 대한 개념을 미리 알고 있어야 글을 이해하기 편할 것 같다.글에서
blessedby-clt.tistory.com
관련해서 이미 글을 쓴 것이 있어 참고해서 봐도 좋을 것 같다.
개인적으로 개입이나 뒷문기준을 이용해서 분석을 했던 경험은 없지만, 여러 인과추론의 주요 개념을 이해하기 위해서는 개입과 뒷문기준에 대한 내용을 숙지할 필요가 있다고는 생각한다.
개념을 설명하기 전에 이 둘을 알아야 하는 이유를 영업(?)해보자면,
- 뒷문기준을 만족하는 변수를 파악하는 과정을 통해, 결론적으로 내가 통제해야 할 공변량을 명확히 파악할 수 있다
- 뒷문기준과 개입 개념을 알아야 성향점수 매칭과 많이 나오는 IPW (Inverse Probability Weighting, 역확률 가중치) 개념을 이해하는데 유리하다.
개입 / 조정공식 / 뒷문기준 / IPW 순으로 개념 설명을 진행해 보겠다!

개입
개입이 필요한 이유
인과관계를 추론하는 것은 "처치에 따라 결과가 어떻게 바뀐다"를 추정하는 것과 같다. 예를 들면 "1시간 더 공부하고 자면(처치) 시험점수는 얼마나 오를까(결과)"라든가, "저속노화 식단을 따라가면(처치) 나의 기대수명은 얼마나 증가할까?(결과)" 같은 질문에 답을 하는 것이다.
처치는 철저한 실험 하에 행해지는 경우도 있겠지만, 관측 데이터를 통해서만 인과효과를 추정해야 하는 상황도 있다. 가령 "게임이 청소년의 폭력성을 높인다"라는 가설을 세우고 인과효과를 추정해 본다고 하자. 실험군과 통제군을 나눠서 단기적으로 실험을 해보는 경우도 있겠지만 윤리적으로 적절한가, 단기간의 실험이 청소년기 전반을 설명할 수 있을까(타당성이 있을까)에 대한 문제에 직면할 수 있다.

무작위 실험이 불가능한 상황에서, 관측 데이터를 기반으로 진짜 인과관계를 추정하고 싶다면 고려해볼 수 있는 선택지가 "개입"이다.
개입의 정의
개입을 조금 쉽게 풀어내면 "변수를 강제로 특정 값으로 고정하는 것"이라고 할 수 있다. 위의 폭력성 실험 상황을 다시 가져와보자.
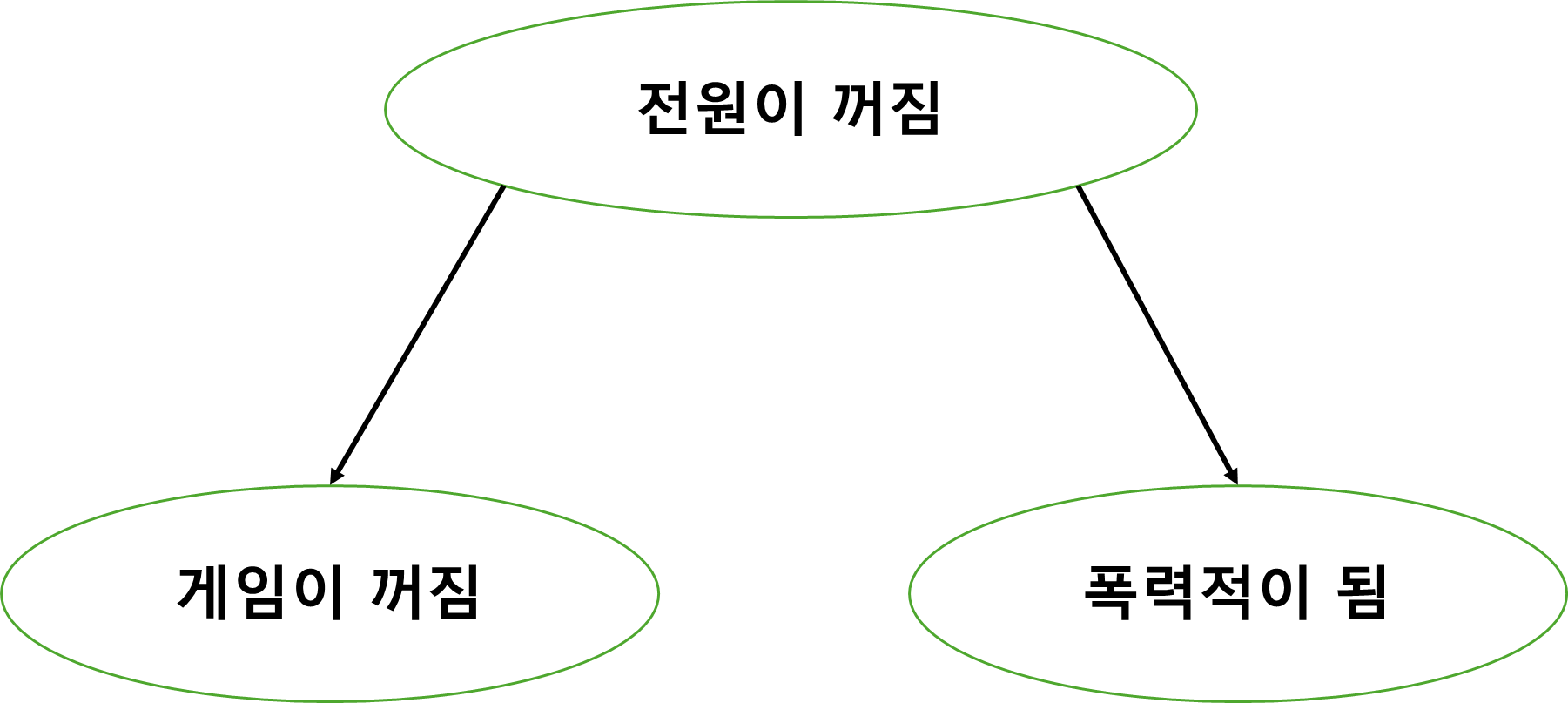
위의 실험상황을 인과 그래프로 표현하면 이렇게 될 것이다. 전원이 꺼지면서 게임이 꺼지고, 또 전원이 꺼지면서 하고 있던 작업물이 날아가서 폭력적이 되어버렸다. 전원이 꺼졌기 때문에 폭력적이 된 것인지, 순간적인 상황 변화를 받아들이지 못하고 폭력 게임의 주인공처럼 난폭하게 변한 것인지... 는 사실 검증을 안 해봐도 알 것 같기는 하지만 일단은 확실하지 않다고 가정해 보자.
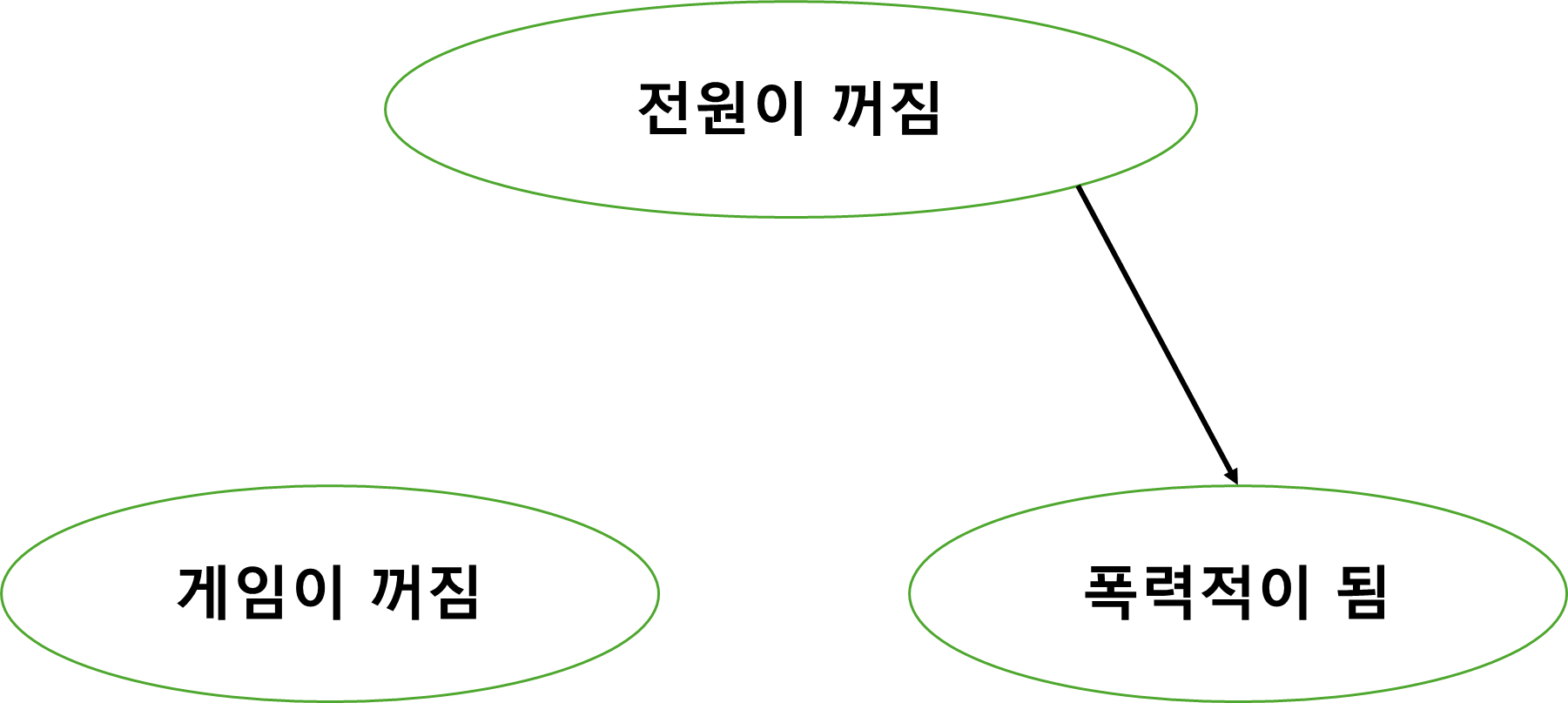
이제 개입을 해보자. 아까 말했듯 변수를 강제로 특정 값으로 고정시켜서 전원이 꺼지거나 말거나 게임은 꺼지지 않는다고 가정해 보자. (게이머에게 일괄 풀충전된 닌텐도로 지급했다고 가정해 보자.)
그러면 전원이 꺼짐과 게임이 꺼짐 사이의 관계는 사라진다. 즉 인과효과를 강제로 끊어낼 수 있다. 그럼에도 여전히 전원이 꺼져서 화가 난 사람들이 있다면 이건 게이머가 아니라 과제를 하고 있던 사람이나 콘서트 티켓팅을 하고 있던 사람일 수 있다. 즉, 게임과 무관하게 갑작스레 중요한 상황에서 누군가 전원을 꺼버렸기 때문에 화가 난 것이므로 게임과 폭력성 간의 관계를 위 실험으로 증명할 수 없다는 뜻이다.
위에서는 조금 느슨하게 표현했지만 개입을 좀 더 엄밀하게 설명하자면, 변수에 직접적인 변화를 가해 시스템 내의 다른 변수들에 미치는 영향을 관찰하는 과정을 의미한다.
개입과 조건부 통제의 차이점
이건 특별한 예시를 들기보다는 "CAUSAL INFERENCE IN STATISTICS: A PRIMER"의 책에 나온 부분을 인용하면 좋을 것 같다.
When we intervene on a variable in a model, we fix its value. We change the system, and the values of other variables often change as a result. When we condition on a variable, we change nothing; we merely narrow our focus to the subset of cases in which the variable takes the value we are interested in. What changes, then, is our perception about the world, not the world itself.
개입은 변수를 강제로 특정 값으로 설정해 시스템의 상태를 변화시키지만, 조건부 통제는 변수 값을 기준으로 하위 그룹을 나누어 해석하는 방법으로, 시스템 자체를 변화시키지는 않는다.
조정공식
개입을 했을 때의 평균 인과 효과를 구할 수 있도록 만들어주는 수식이 조정공식(adjustment formula)이다. 처치변수와 결과변수 사이의 인과 효과를 추정하는 공식으로, 관찰 연구에서 개입 후의 인과적 영향을 추정할 때 유용한 도구라 할 수 있다.
- X : 과거 1년 이내 건강검진 여부
- Y : 이후 3년 내 병원 입원 여부
- Z : 연령
이런 변수가 있다고 가정해 보자.
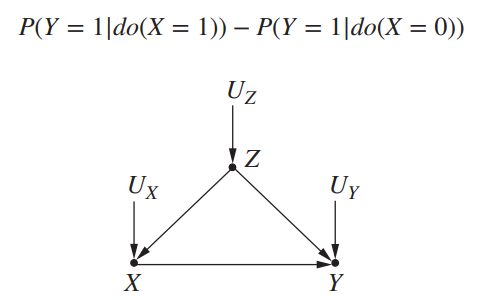
건강검진 여부가 건강에 긍정적인 영향을 미치는지를 알고 싶은데, "연령" 이 높을수록 일반적으로 건강검진을 더 받게 되고, "연령"이 높을수록 만성질환 등의 영향으로 건강이 나빠져 병원에 입원할 가능성이 더 크다. 그래서 대충 보고 판단하면 "건강검진"이 "사람을 병원에 입원시킨다"라는 잘못된 결론에 빠질 수 있게 된다.
즉, 현재 내가 관심 있는 건 X가 Y에 미치는 효과인데 Z가 X, Y에 모두 영향을 미치고 있어서 인과효과를 추정하기 어렵다. 이때 X에 대한 개입을 한다고 하면 X의 값을 특정 값으로 "강제"로 고정시킬 수 있게 된다.
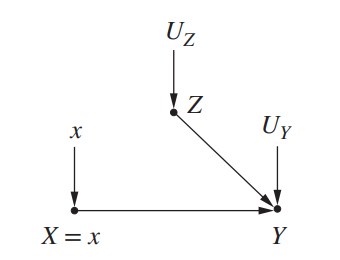
강제로 X의 값을 고정시켜 버렸기 때문에 X는 더 이상 Z에 영향을 받지 않게 된다. X에 개입을 한다면 \( do(X=x) \)로 표기할 수 있다.
평균인과효과(Average Causal Effect)는 사람들 모두를 강제로 건강검진을 받도록 만들었을 때의 병원에 입원할 확률과 사람들 모두를 강제로 건강검진을 받지 못하게 만들었을 때의 병원에 입원할 확률의 차이로 구할 수 있다. 그렇지만 현실적으로 이런 처치가 불가능하기 때문에 조정공식을 사용한다.
조정공식을 구하기 전에 2가지를 알아야 한다.
- 개입을 하건 하지 않건 \(P(Y = y | X = x, Z = z)\) 는 변하지 않는다. Y로 들어오는 화살표만 놓고 보면 개입을 하기 전과 후의 차이가 없기 때문에 조건부 확률은 변하지 않는다.
- \(P(Z=z|X=x)\)는 \(P(Z=z)\)와 같다. Z에 X가 영향을 미치지 않기 때문이다.
\(P(Y | do(X=x)) = \sum_{z} P_m(Y | Z, X)* P_m(Z | X) \)의 형태로 쓸 수 있는데, (\(P_m\)은 X에 개입을 시킨 상태라는 뜻이다.)
위에 정의한 수식을 그대로 대입하면 개입을 하지 않았을 때의 조건부 확률을 바탕으로 강제로 개입시켰을 때의 인과효과를 구할 수 있게 된다. 즉, X를 어떻게 지지고 볶든 Z라는 공변량을 기반으로 조건부 확률을 구성하면 원래의 데이터 셋을 기반으로 인과효과를 추정할 수 있게 된다는 뜻이다. 그리고 Z라는 공변량은 뒷문기준을 만족해야 한다.
뒷문기준
뒷문기준(backdoor criterion)은 X와 Y 사이의 인과효과를 파악하는데 방해가 되는 경로를 의미한다. 건강검진이 병원 입원에 미치는 영향력을 파악하는데 "연령"이라는 변수가 방해를 하는 상황을 다시 가져와보자. 건강검진 → 입원 여부라는 경로 이외에 건강검진 ← 연령 → 입원 여부라는 경로가 추가로 열려 있어 인과효과를 파악하는데 방해가 된다.
뒷문기준을 좀 더 정확하게 정의한다면 다음과 같다.
(X, Y)가 주어졌을 때, X의 자손이 Z에 있는 어떤 노드에도 포함되지 않으면서 Z가 X로 향하는 모든 경로를 차단할 때 Z는 X의 뒷문기준을 만족한다고 한다.
개입을 할 때에는 뒷문기준을 만족하는 변수를 조정해야 한다. 뒷문기준을 만족하는 변수는 X와 Y 간 허위 경로를 차단하는 역할을 하므로 이를 통제하여 인과 효과를 명확하게 추정할 수 있다.
이러면 뒷문기준은 다음과 같은 조건을 만족한다.
1. Z를 막으면 X와 Y 사이의 허위 경로를 모두 막을 수 있다.
2. Z를 막더라도 X와 Y 사이에 직접 연결된 경로는 그대로 남겨두어야 한다.
3. Z를 막았을 때 새로운 허위경로가 생겨서는 안 된다.
쉽게 풀어쓰면 X와 Y 사이에 X와 Y에 동시에 영향을 주는 Z 변수(fork)가 있다면 대충 뒷문기준을 만족한다고 봐도 되고, 대신 X와 Y가 동시에 영향을 주는 Z 변수(collider)가 있다면 조금 의심해서 봐야 한다고 쓸 수 있다.
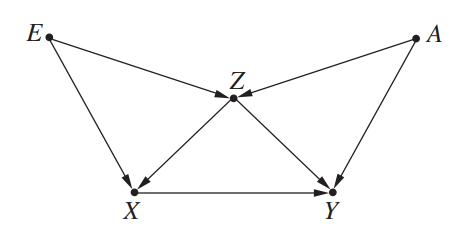
이런 그래프가 있고 X와 Y 사이의 뒷문기준을 만족하는 변수를 찾는다고 해보자. X와 Y 사이에 동시에 영향을 미치는 변수는 Z이다. (화살표가 동시에 뻗어있다.) 그러나 Z는 E와 A에 영향을 받는데(collider), E는 X에, A는 Y에 영향을 주므로 Z만을 막으면 X ← E ← Z → A → Y라는 새로운 허위경로가 열리게 된다. E 또는 A를 함께 조정해 주면 허위경로가 다시 닫히게 되므로 뒷문기준을 만족하는 변수 집합은 {E, Z}, {A, Z}, {A, E, Z}가 된다.
역확률가중치
역확률 가중치(Inverse Probability Weighting, 이하 IPW) 라 함은 처치확률(일반적으로 성향점수를 넣음)의 역수를 가중치로 곱해서 편향을 조정하는 것으로 알려져 있다. 성향점수의 역수를 곱한다..는 게 직관적으로 딱 와닿지는 않는데 따지고 보면 역확률 가중치는 조정공식을 변형한 식이다.

앞서 \(P(Y | do(X=x)) = \sum_{z} P(Y | Z, X)* P(Z)\) 로 쓸 수 있다고 했다. 조건부 확률을 이렇게 저렇게 만지면
\(P(Y | Z, X) = \frac{P(X, Y, Z)}{P(X, Z)}\) 로 바꿔쓸 수 있고
분모에 들어간 \(P(X, Z) = P(X | Z)P(Z)\)로 바꿔쓸 수 있다.
각각을 식에 대입하면 \(P(Y | do(X=x)) = \frac{P(X, Y, Z)}{P(X|Z)} \)가 되는데 이 때 \(P(X|Z)\)가 처치확률, 즉 성향점수가 된다. 조정공식을 통해 자연스럽게 결합확률(joint probability)에 성향점수를 나눈 값, 즉 역확률 가중치를 곱해준 값을 얻을 수 있게 되는 것이다.
좀 더 정리하면,
- 우리는 X의 값을 강제로 고정시키는 개입을 했고, ( \(P(Y | do(X = x))\) )
- 개입을 통한 평균 인과효과를 구하기 위해 조정공식을 사용했다.
- 우리가 조정공식에 사용할 수 있는 변수는 X와 Y의 뒷문기준을 만족해야 한다.
- 조정공식을 변형하면 역확률가중치의 수식을 구할 수 있다.
역확률 가중치는 "개입"이라는 프레임워크에서 나온 것이라는 것에 주목해야 한다. 개입은 처치변수 X의 값을 강제로 고정시키는 작업이다.
● ○ ○ ○ ○ (검은색 동그라미가 처치, 흰색 동그라미가 미처치)
이런 상태라고 할 때 강제로 다 검은색을 만들어주려면 검은색이 나올 확률인 1/5의 역수를 곱해주면 된다. 그러면 검은색 동그라미 5개를 만들 수 있다. 반대로 강제로 다 흰색을 만들어주기 위해서는 흰색이 나올 확률인 5/4의 역수를 곱해주면 된다. 그러면 흰색 동그라미 5개를 만들 수 있다. (각각 역확률 가중치)
또한, 역확률 가중치는 개입 및 조정공식의 변형이기 때문에 뒷문기준을 만족하지 못하는 변수를 성향점수에 넣어서 계산하면 편향이 발생할 수 있음에 유의해야 한다.
뒷문기준에 유의하여 역확률 가중치에 접근한다면 좀 더 알잘딱한 분석이 나올 수 있지 않을까 생각해본다.
참고자료
- 통계적 인과추론(CAUSAL INFERENCE IN STATISTICS: A PRIMER)
'Statistics' 카테고리의 다른 글
| 베이지안 통계 - 기본 개념 가볍게 살펴보기 (0) | 2025.01.12 |
|---|---|
| 가상의 게임 데이터로 살펴보는 이중차분법 (feat. 🧙♂️법사야캐요) (0) | 2024.12.30 |
| 인과추론 학습기 - SCM과 인과 그래프 (3) | 2024.10.19 |
| 인과추론을 위한 회귀분석 개념 정리 - 편회귀계수, FWL 정리 (2) | 2024.04.21 |
| 매칭(Matching)을 통한 인과추론 : 개념부터 실습까지 (feat. ChatGPT) (2) | 2024.03.25 |
