1. 사건의 전말
통계학과를 졸업하기는 했지만, 관련 전공 지식을 별로 사용할 일은 없었다.
하여 k means clustering도 이론으로만 어렴풋이 알고 있을 뿐, 관련해서 깊게 생각해본 적도 없었다.
알음알음 전공 수업을 듣거나, ADsP나 ADP 필기 공부하면서 알고 있는 내용이라고는
- 비지도 학습의 일종이다.
- 임의로 할당한 초깃값을 갖고 알고리즘을 시작, 각 레코드를 초깃값에 가장 가까운 평균을 갖는 클러스터에 레코드를 할당하는 방식으로 분류
- 이상치에 영향을 많이 받으며, 최적 군집 수를 직접 찾아줘야 한다.
이 정도였다.
그러던 중, 최근 R&D 성격의 업무를 하면서, '데이터를 군집분석을 통해 좀 세분화해서 보면 좋지 않을까?'라는 생각에 kmeans clustering을 시도했었다.
작업할 때는 혼자 뭔가 배웠던 이론을 직접 실습해본다는 것에 취해서 몰랐는데, 자료를 검토하신 팀장님께서 여쭤보신 질문에 대답을 할 수 없었던 것들이 너무 많아서.. 군집분석을 만만하게 보고, 무분별하게 사용했다는 생각에 공부하게 되었다.
2. 팀장님의 질문
일단, 회사에서 사용한 데이터를 사용할 수는 없으니, 가장 기초적인 iris 데이터를 사용해서 상황을 설명하면 다음과 같다. (※ 글이 너무 길어질 것 같아서 iris 데이터에 대한 설명은 과감하게 패스해본다.)
R에서는 군집분석에 대한 최적군집을 찾아주는 라이브러리가 있다.
Nbclust::NbClust(iris[,c(1:4)], distance = "euclidean", min.nc = 2, max.nc = 10, method = "kmeans")
NbClust 라이브러리를 설치하고, 이대로 실행시키면 NbClust에 내재(?)된 여러가지 기준으로 최적 군집수를 판단해 준다.

해당 명령어를 입력하면, 이런 식으로 자체적으로 결론을 내주는데,
문제는 저 위에 노란색으로 표시한 글은 읽어볼 생각은 하지도 않았단 것..

암만 인공지능 시대라, 추천해주는대로 따라가면 된다지만 팀장님께서 '저 Dindex가 뭐에요?'라고 질문하셨을 때 대답도 못하는 건 어쩐지 분석을 공부하는 사람 입장에서 부끄럽다는 생각이 들었다.
한 가지 더 부끄러웠던 것도 같이 언급해본다.
저 명령어를 입력하면
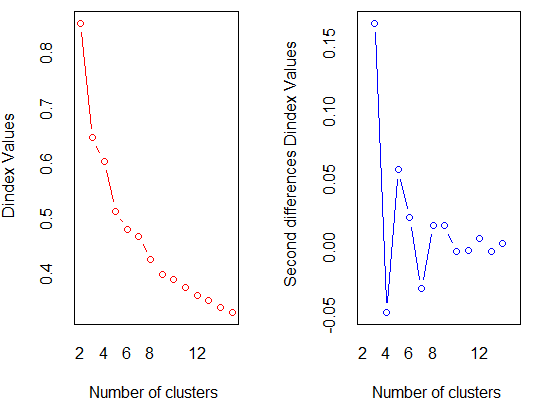
이런 식으로 그래프도 뽑는데, Dindex가 아니라 WSS(within groups sum of Squares)로 보고 해석했다는 게 부끄러울 노릇이다.
하룻강아지가 범 무서운줄 모른다지만, 아무리 애송이라도 Dindex 무서운 줄 모르고 막 쓰면 안 되지 않을까..?
그리고 이 데이터는 굉장히 Species에 따른 관측변수의 특징이 뚜렷하게 나타나는 편이고, 단위도 일치하여 Scaling을 고려할 필요가 없는데, 현실의 데이터는 그리 녹록치 않다.
일단 데이터마다 단위가 다르기 때문에 Scaling을 해줘야 한다. 관측치 간 거리를 계산하는 k means 알고리즘 특성 상 데이터의 단위가 다르면 단위가 큰 변수의 영향력이 커지기 때문이다.
당시 나는 Z score 밖에 몰랐기 때문에 연속형 변수에 대해 Z-score Scaling을 다 돌려서 작업을 했었는데,
문제는 min-max Scaling도 엄연히 존재하건만, 선택지에 고려조차 하지 않았다는 것이다.
더 심각한 건, 내가 쪼개려고 시도했던 데이터는 값이 한 쪽에 쏠려있는 Skewed data였는데, Skewed Data에 대해서도 Normalizing이나 min-max를 써도 되는지를 알 수 없었다는 것이다.
그래서 팀장님께서 "한 쪽으로 데이터가 쏠리면 로그 변환을 해서 Scaling을 해줘야 하나요?"라고 여쭤보셨을 때 대답할 수 없었다.
결국, 너무 안일했던 내 자신을 반성하며
- Dindex 란 무엇인가?
- skewed 데이터에는 로그 변환 후 scaling을 시켜야 하는가?
에 대한 부분을 찾아보게 되었다.
3. D index란 무엇인가?
처음에는 팀장님께서 여쭤보셨을 때 순간 "Dunn index가 아닐까요?"라고 말씀드렸는데, 이번에 찾아보니 D로 시작하는 index가 여러 개 된다는 사실을 알게 되었다.
그 때부터 시작된 나의 고민은
1. 이 중 뭐가 Dindex인거지?
2. index는 도대체 뭔 index라는 거지?
이 두 가지였다.
이 중 2번에 대한 부분을 먼저 정리해본다.
아무리 데이터를 클러스터링하더라도, (나처럼) '데이터를 분류해냈어!' 하고 만족하고 끝나는 게 아니라 클러스터링이 잘 된 건지 혹은 아닌지를 판단하는 기준이 필요하다.
좋은 군집이라 함은 무릇 군집 내 관측치끼리는 거리가 가까워야 하며, 군집 간에는 거리가 멀어야 하는데,
그걸 판단할 수 있도록 도와주는 기준이 index라고 할 수 있겠다.
그리고 대부분의 데이터 과학이 그러하듯, 모형 내에서 이 군집이 좋은 군집인지를 판단하는 방법이 있고, 모형 밖에서 일반적으로 알려진 사실이라던가, 전문가의 견해라든가.. benchmark와 일치하는지를 비교하여 판단하는 방법이 있다.
그리고 내가 찾은 여러 개의 Dindex는 모두 모형 내에서 판단하는 기준의 일종이다.
1. Dunn index : 최소한의 군집 간 거리, 최대의 군집 간 거리의 비율. 군집 안에서는 높은 유사성을 갖고, 군집 간에는 최대한 이질적인 군집을 찾기 때문에 높을 수록 이상적임.
2. Davies-Bouldin Index : A, B 군집에 대해 각 군집 내 거리의 합을 각 군집 중심 간 거리로 나눈 값으로 표현. 낮을 수록 이상적임.
3. Dindex : 놀랍게도 R에서 사용하는 Dindex가 따로 있었다!! 군집 내의 유사성을 판단하는 index의 일종인데, 군집 별로 군집 내 중심과 떨어진 거리를 평균낸 값을 군집 개수를 늘려가면서 기록.(결국 낮을 수록 이상적임). q-1개 일 때의 값과 q개일 때의 값을 비교해서 이 값이 제일 작을 때를 선택.
이제야 R에서 'the significant peak in Dindex second differences plot'가 뾰족해지는 지점을 왜 고르라는지는 어렴풋이 알 것 같다. (q-1)일 때의 값과 q일 때의 값을 뺀 게 작은 지점을 선택한다는 건, 결국 q일 때의 값과 q+1일 때의 값을 뺀 건 앞의 값보다 커지기 때문에 Seconde differences plot으로 그리면 뾰족해지지 않을까..?라는 느낌적인 느낌.
(사실 잘 모르겠다.)
아무튼 R에서 말하는 Dindex는 Dunn index도, Davies-Bouldin index도 아닌 제 3의 인덱스였다는 것.
4. Skewed data에서의 Scaling
결론부터 말하면 이건 잘 모르겠다..
열심히 구글링을 해본 결과, 어떤 곳에서는 Skewed data일 경우 로그 변환 시켜서 클러스터링을 하라고는 하는데, skewed data에 0이나 음수가 포함되면 이 변환 자체를 사용할 수 없다는 것이 문제다.
또 내 상식 선에서는 어쨌든 Scaling의 목적은 각 magnitude의 영향력을 통일시킨다는 느낌인데, 어쨌든 'Skewed data라도 min-max나 z-score로 표준화를 시키면 변수 간 영향력은 통제되지 않나? skewed의 여부도 클러스터링에 영향을 줄 수 있는건가?'라는 생각이 들었다.
데이터 대부분이 다 0에 쏠리고, 벗어난 나머지 값에 대해서는 다 이상치로 인식하게 돼서 영향을 받는건가 싶기도 했지만 여기까지 참고할만한 레퍼런스를 찾지는 못했기 때문에 잘 모르겠다가 결론이다.
대신 iris 데이터로 실험을 해보기는 했는데..
library(sn)
data(iris)
str(iris)
set.seed(1777)
iris<- iris%>%mutate(test = ifelse(Species=="virginica",
rsn(n=length(which(iris$Species=="virginica")), xi=1.7777, omega=2.1111, alpha=10),
ifelse(Species=="setosa", rsn(n=length(which(iris$Species=="setosa")), xi=2.7777, omega=2.1111, alpha=10),
rsn(n=length(which(iris$Species=="versicolor")), xi=3.7777, omega=2.1111, alpha=10))))
이런 식으로 skewed data를 만드는 난수를 iris 데이터에 붙여주었다.
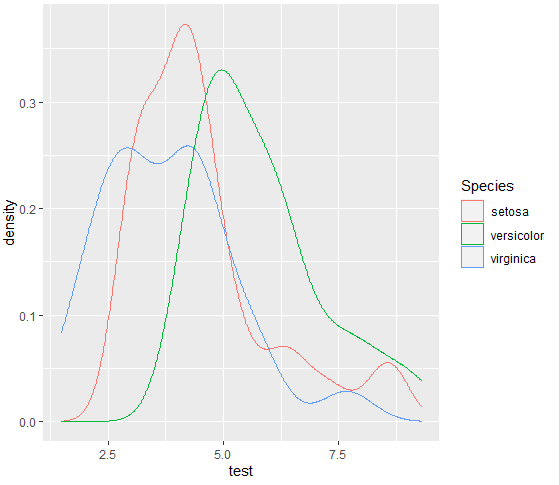
그러면 Species 별로 미묘하게 분포가 다른 skewed 난수가 만들어진다.
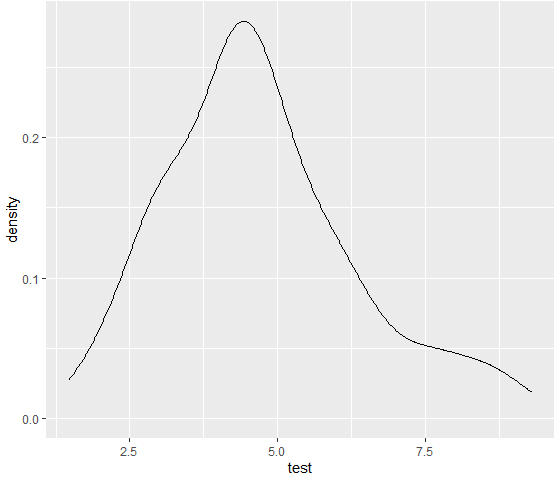
종 구분 없이 밀도함수를 그리면 애매하긴 한데 어쨌든 조금은 skewed한 모습이다.
이 상태로
1. z-score scaling
2. min-max scaling
3. test 변수를 log변환한 후 z-score scaling
한 후, 군집 3개로 kmeans clustering 한 결과를 실제 종과 비교해보기로 했다.
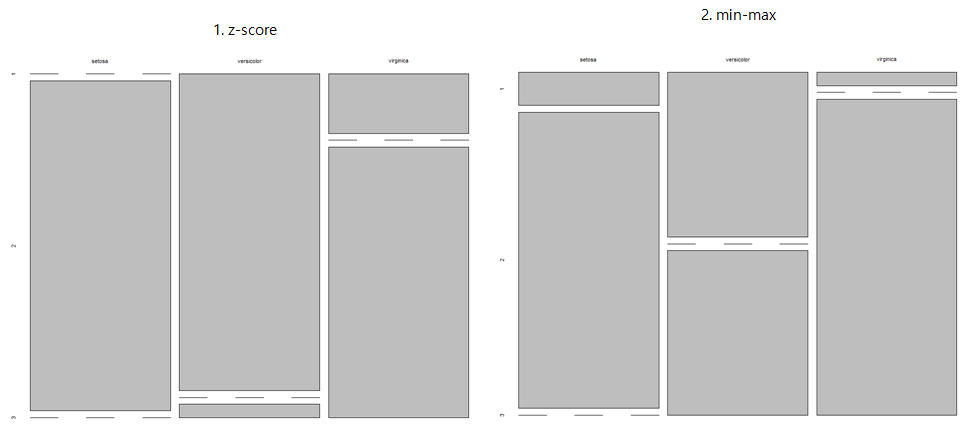

일단 1차로 실험해본 결과 log 변환을 시켜준 게 분류 자체는 제일 잘 된 것처럽 보이는데
(1. z-score만 한 건 3번째 종의 분류가 여러 군집으로 많이 혼재되어 있고, min-max는 2번째 종의 분류가 거의 제대로 되지 않았다.)
그렇다고 이걸 skewed data에는 무조건 로그 변환을 해야합니다! 라고 말하기도 어렵다..
Scaling도 무조건 한 방법만 쓸 게 아니라, 더 확실하게 EDA를 진행한 후, 여러 방법으로 돌려봐야 할 것 같다는 게 결론이다.
참고링크 :
1. 정규화
hleecaster.com/ml-normalization-concept/
정규화(Normalization) 쉽게 이해하기 - 아무튼 워라밸
데이터 정규화는 머신러닝에서 꼭 알아야 하는 개념이다. 매우 훌륭한 데이터를 가지고도 정규화를 놓치면 특정 feature가 다른 feature들을 완전히 지배할 수 있기 때문이다. 최소 최대 정규화, Z-
hleecaster.com
2. index 관련
Clustering Evaluation and assessment
클러스터링 결과의 평가는 cluster validation이라고도 한다. 두 클러스터링 간 유사도 측정에 대한 몇가지 제안들이 있다. 이러한 측정법은 한 데이터 셋에서 작동하는 데이터 클러스터링 알고리즘
gentlej90.tistory.com
www.geeksforgeeks.org/dunn-index-and-db-index-cluster-validity-indices-set-1/
Dunn index and DB index - Cluster Validity indices | Set 1 - GeeksforGeeks
A Computer Science portal for geeks. It contains well written, well thought and well explained computer science and programming articles, quizzes and practice/competitive programming/company interview Questions.
www.geeksforgeeks.org
226 Dindex The Dindex Lebart et al 2000 is based on clustering gain on intra | Course Hero
226 Dindex The Dindex Lebart et al 2000 is based on clustering gain on intra from CSE 7331 at Southern Methodist University
www.coursehero.com
Davies-Bouldin Index(DBI)
Davies-Bouldin Index(DBI)는 Group 내에서의 Distribution과 비교하여 다른 Group간의 분리 정도의 비율로 계산되는 값으로 모든 두 개의 Group 쌍에 대해 각 Group의 크기의 합을 각 Group의 중심 간 거리로..
elecs.tistory.com
3. skewed data에 대한 처리
Should k-means only be applied if the variables are normally distributed?
I have a complex data set with various features, some of them are not normally distributed (e.g. very skewed to the left). Is it genereally advisable to make these variables normal distributed (Gau...
stats.stackexchange.com
Clustering data - data transformation (log2) highly improves clustering but why?
• link • Not following modified 3.1 years ago • written 3.1 years ago by JJ • 520
www.biostars.org
'Statistics' 카테고리의 다른 글
| 수리통계학 - MLE와 MVUE에 대하여 (2) | 2021.08.28 |
|---|---|
| 수리통계학 - 추정량을 선택하는 기준에 대하여 (0) | 2021.08.10 |
| 시계열 분석 - ARIMA 모형 정리 (0) | 2021.04.17 |
| 헷갈리는 회귀분석의 기록(2) - 회귀분석 모형 진단 (0) | 2021.02.07 |
| 헷갈리는 회귀분석의 기록(1) - 회귀분석의 가정 및 결정계수의 의미 (0) | 2020.11.09 |
1. 사건의 전말
통계학과를 졸업하기는 했지만, 관련 전공 지식을 별로 사용할 일은 없었다.
하여 k means clustering도 이론으로만 어렴풋이 알고 있을 뿐, 관련해서 깊게 생각해본 적도 없었다.
알음알음 전공 수업을 듣거나, ADsP나 ADP 필기 공부하면서 알고 있는 내용이라고는
- 비지도 학습의 일종이다.
- 임의로 할당한 초깃값을 갖고 알고리즘을 시작, 각 레코드를 초깃값에 가장 가까운 평균을 갖는 클러스터에 레코드를 할당하는 방식으로 분류
- 이상치에 영향을 많이 받으며, 최적 군집 수를 직접 찾아줘야 한다.
이 정도였다.
그러던 중, 최근 R&D 성격의 업무를 하면서, '데이터를 군집분석을 통해 좀 세분화해서 보면 좋지 않을까?'라는 생각에 kmeans clustering을 시도했었다.
작업할 때는 혼자 뭔가 배웠던 이론을 직접 실습해본다는 것에 취해서 몰랐는데, 자료를 검토하신 팀장님께서 여쭤보신 질문에 대답을 할 수 없었던 것들이 너무 많아서.. 군집분석을 만만하게 보고, 무분별하게 사용했다는 생각에 공부하게 되었다.
2. 팀장님의 질문
일단, 회사에서 사용한 데이터를 사용할 수는 없으니, 가장 기초적인 iris 데이터를 사용해서 상황을 설명하면 다음과 같다. (※ 글이 너무 길어질 것 같아서 iris 데이터에 대한 설명은 과감하게 패스해본다.)
R에서는 군집분석에 대한 최적군집을 찾아주는 라이브러리가 있다.
Nbclust::NbClust(iris[,c(1:4)], distance = "euclidean", min.nc = 2, max.nc = 10, method = "kmeans")
NbClust 라이브러리를 설치하고, 이대로 실행시키면 NbClust에 내재(?)된 여러가지 기준으로 최적 군집수를 판단해 준다.

해당 명령어를 입력하면, 이런 식으로 자체적으로 결론을 내주는데,
문제는 저 위에 노란색으로 표시한 글은 읽어볼 생각은 하지도 않았단 것..

암만 인공지능 시대라, 추천해주는대로 따라가면 된다지만 팀장님께서 '저 Dindex가 뭐에요?'라고 질문하셨을 때 대답도 못하는 건 어쩐지 분석을 공부하는 사람 입장에서 부끄럽다는 생각이 들었다.
한 가지 더 부끄러웠던 것도 같이 언급해본다.
저 명령어를 입력하면

이런 식으로 그래프도 뽑는데, Dindex가 아니라 WSS(within groups sum of Squares)로 보고 해석했다는 게 부끄러울 노릇이다.
하룻강아지가 범 무서운줄 모른다지만, 아무리 애송이라도 Dindex 무서운 줄 모르고 막 쓰면 안 되지 않을까..?
그리고 이 데이터는 굉장히 Species에 따른 관측변수의 특징이 뚜렷하게 나타나는 편이고, 단위도 일치하여 Scaling을 고려할 필요가 없는데, 현실의 데이터는 그리 녹록치 않다.
일단 데이터마다 단위가 다르기 때문에 Scaling을 해줘야 한다. 관측치 간 거리를 계산하는 k means 알고리즘 특성 상 데이터의 단위가 다르면 단위가 큰 변수의 영향력이 커지기 때문이다.
당시 나는 Z score 밖에 몰랐기 때문에 연속형 변수에 대해 Z-score Scaling을 다 돌려서 작업을 했었는데,
문제는 min-max Scaling도 엄연히 존재하건만, 선택지에 고려조차 하지 않았다는 것이다.
더 심각한 건, 내가 쪼개려고 시도했던 데이터는 값이 한 쪽에 쏠려있는 Skewed data였는데, Skewed Data에 대해서도 Normalizing이나 min-max를 써도 되는지를 알 수 없었다는 것이다.
그래서 팀장님께서 "한 쪽으로 데이터가 쏠리면 로그 변환을 해서 Scaling을 해줘야 하나요?"라고 여쭤보셨을 때 대답할 수 없었다.
결국, 너무 안일했던 내 자신을 반성하며
- Dindex 란 무엇인가?
- skewed 데이터에는 로그 변환 후 scaling을 시켜야 하는가?
에 대한 부분을 찾아보게 되었다.
3. D index란 무엇인가?
처음에는 팀장님께서 여쭤보셨을 때 순간 "Dunn index가 아닐까요?"라고 말씀드렸는데, 이번에 찾아보니 D로 시작하는 index가 여러 개 된다는 사실을 알게 되었다.
그 때부터 시작된 나의 고민은
1. 이 중 뭐가 Dindex인거지?
2. index는 도대체 뭔 index라는 거지?
이 두 가지였다.
이 중 2번에 대한 부분을 먼저 정리해본다.
아무리 데이터를 클러스터링하더라도, (나처럼) '데이터를 분류해냈어!' 하고 만족하고 끝나는 게 아니라 클러스터링이 잘 된 건지 혹은 아닌지를 판단하는 기준이 필요하다.
좋은 군집이라 함은 무릇 군집 내 관측치끼리는 거리가 가까워야 하며, 군집 간에는 거리가 멀어야 하는데,
그걸 판단할 수 있도록 도와주는 기준이 index라고 할 수 있겠다.
그리고 대부분의 데이터 과학이 그러하듯, 모형 내에서 이 군집이 좋은 군집인지를 판단하는 방법이 있고, 모형 밖에서 일반적으로 알려진 사실이라던가, 전문가의 견해라든가.. benchmark와 일치하는지를 비교하여 판단하는 방법이 있다.
그리고 내가 찾은 여러 개의 Dindex는 모두 모형 내에서 판단하는 기준의 일종이다.
1. Dunn index : 최소한의 군집 간 거리, 최대의 군집 간 거리의 비율. 군집 안에서는 높은 유사성을 갖고, 군집 간에는 최대한 이질적인 군집을 찾기 때문에 높을 수록 이상적임.
2. Davies-Bouldin Index : A, B 군집에 대해 각 군집 내 거리의 합을 각 군집 중심 간 거리로 나눈 값으로 표현. 낮을 수록 이상적임.
3. Dindex : 놀랍게도 R에서 사용하는 Dindex가 따로 있었다!! 군집 내의 유사성을 판단하는 index의 일종인데, 군집 별로 군집 내 중심과 떨어진 거리를 평균낸 값을 군집 개수를 늘려가면서 기록.(결국 낮을 수록 이상적임). q-1개 일 때의 값과 q개일 때의 값을 비교해서 이 값이 제일 작을 때를 선택.
이제야 R에서 'the significant peak in Dindex second differences plot'가 뾰족해지는 지점을 왜 고르라는지는 어렴풋이 알 것 같다. (q-1)일 때의 값과 q일 때의 값을 뺀 게 작은 지점을 선택한다는 건, 결국 q일 때의 값과 q+1일 때의 값을 뺀 건 앞의 값보다 커지기 때문에 Seconde differences plot으로 그리면 뾰족해지지 않을까..?라는 느낌적인 느낌.
(사실 잘 모르겠다.)
아무튼 R에서 말하는 Dindex는 Dunn index도, Davies-Bouldin index도 아닌 제 3의 인덱스였다는 것.
4. Skewed data에서의 Scaling
결론부터 말하면 이건 잘 모르겠다..
열심히 구글링을 해본 결과, 어떤 곳에서는 Skewed data일 경우 로그 변환 시켜서 클러스터링을 하라고는 하는데, skewed data에 0이나 음수가 포함되면 이 변환 자체를 사용할 수 없다는 것이 문제다.
또 내 상식 선에서는 어쨌든 Scaling의 목적은 각 magnitude의 영향력을 통일시킨다는 느낌인데, 어쨌든 'Skewed data라도 min-max나 z-score로 표준화를 시키면 변수 간 영향력은 통제되지 않나? skewed의 여부도 클러스터링에 영향을 줄 수 있는건가?'라는 생각이 들었다.
데이터 대부분이 다 0에 쏠리고, 벗어난 나머지 값에 대해서는 다 이상치로 인식하게 돼서 영향을 받는건가 싶기도 했지만 여기까지 참고할만한 레퍼런스를 찾지는 못했기 때문에 잘 모르겠다가 결론이다.
대신 iris 데이터로 실험을 해보기는 했는데..
library(sn)
data(iris)
str(iris)
set.seed(1777)
iris<- iris%>%mutate(test = ifelse(Species=="virginica",
rsn(n=length(which(iris$Species=="virginica")), xi=1.7777, omega=2.1111, alpha=10),
ifelse(Species=="setosa", rsn(n=length(which(iris$Species=="setosa")), xi=2.7777, omega=2.1111, alpha=10),
rsn(n=length(which(iris$Species=="versicolor")), xi=3.7777, omega=2.1111, alpha=10))))
이런 식으로 skewed data를 만드는 난수를 iris 데이터에 붙여주었다.

그러면 Species 별로 미묘하게 분포가 다른 skewed 난수가 만들어진다.

종 구분 없이 밀도함수를 그리면 애매하긴 한데 어쨌든 조금은 skewed한 모습이다.
이 상태로
1. z-score scaling
2. min-max scaling
3. test 변수를 log변환한 후 z-score scaling
한 후, 군집 3개로 kmeans clustering 한 결과를 실제 종과 비교해보기로 했다.


일단 1차로 실험해본 결과 log 변환을 시켜준 게 분류 자체는 제일 잘 된 것처럽 보이는데
(1. z-score만 한 건 3번째 종의 분류가 여러 군집으로 많이 혼재되어 있고, min-max는 2번째 종의 분류가 거의 제대로 되지 않았다.)
그렇다고 이걸 skewed data에는 무조건 로그 변환을 해야합니다! 라고 말하기도 어렵다..
Scaling도 무조건 한 방법만 쓸 게 아니라, 더 확실하게 EDA를 진행한 후, 여러 방법으로 돌려봐야 할 것 같다는 게 결론이다.
참고링크 :
1. 정규화
hleecaster.com/ml-normalization-concept/
정규화(Normalization) 쉽게 이해하기 - 아무튼 워라밸
데이터 정규화는 머신러닝에서 꼭 알아야 하는 개념이다. 매우 훌륭한 데이터를 가지고도 정규화를 놓치면 특정 feature가 다른 feature들을 완전히 지배할 수 있기 때문이다. 최소 최대 정규화, Z-
hleecaster.com
2. index 관련
Clustering Evaluation and assessment
클러스터링 결과의 평가는 cluster validation이라고도 한다. 두 클러스터링 간 유사도 측정에 대한 몇가지 제안들이 있다. 이러한 측정법은 한 데이터 셋에서 작동하는 데이터 클러스터링 알고리즘
gentlej90.tistory.com
www.geeksforgeeks.org/dunn-index-and-db-index-cluster-validity-indices-set-1/
Dunn index and DB index - Cluster Validity indices | Set 1 - GeeksforGeeks
A Computer Science portal for geeks. It contains well written, well thought and well explained computer science and programming articles, quizzes and practice/competitive programming/company interview Questions.
www.geeksforgeeks.org
226 Dindex The Dindex Lebart et al 2000 is based on clustering gain on intra | Course Hero
226 Dindex The Dindex Lebart et al 2000 is based on clustering gain on intra from CSE 7331 at Southern Methodist University
www.coursehero.com
Davies-Bouldin Index(DBI)
Davies-Bouldin Index(DBI)는 Group 내에서의 Distribution과 비교하여 다른 Group간의 분리 정도의 비율로 계산되는 값으로 모든 두 개의 Group 쌍에 대해 각 Group의 크기의 합을 각 Group의 중심 간 거리로..
elecs.tistory.com
3. skewed data에 대한 처리
Should k-means only be applied if the variables are normally distributed?
I have a complex data set with various features, some of them are not normally distributed (e.g. very skewed to the left). Is it genereally advisable to make these variables normal distributed (Gau...
stats.stackexchange.com
Clustering data - data transformation (log2) highly improves clustering but why?
• link • Not following modified 3.1 years ago • written 3.1 years ago by JJ • 520
www.biostars.org
'Statistics' 카테고리의 다른 글
| 수리통계학 - MLE와 MVUE에 대하여 (2) | 2021.08.28 |
|---|---|
| 수리통계학 - 추정량을 선택하는 기준에 대하여 (0) | 2021.08.10 |
| 시계열 분석 - ARIMA 모형 정리 (0) | 2021.04.17 |
| 헷갈리는 회귀분석의 기록(2) - 회귀분석 모형 진단 (0) | 2021.02.07 |
| 헷갈리는 회귀분석의 기록(1) - 회귀분석의 가정 및 결정계수의 의미 (0) | 2020.11.09 |
