들어가며
베이지안 통계를 한 마디로 가볍게 설명하면 나의 사전분포와 데이터에 기반한 증거를 기반으로, 사후분포를 갱신한 후 사후분포에서 모수가 어떻게 되는지를 추정하는 것이라 할 수 있다. 사전분포와 likelihood를 알면 바로 사후분포를 정의할 수 있는 경우, 즉 conjugate 한 경우는 앞에서 말했듯 사후분포를 바로 정의할 수 있기 때문에 모수를 추정하는 것이 쉬운 일이 된다. (conjugate에 대한 설명은 해당 링크를 참고해주시면 감사하겠습니다 땡큐)
그러나 사후분포를 계산하는 것이 어렵거나, 사후분포 자체를 정의하기 어려운 경우에는 시뮬레이션을 사용하게 되는데 이때 대표적으로 사용하는 방법이 MC(Monte Carlo), Gibbs Sampler, Metropolis 알고리즘이다.

이 글에서는 위 3개 알고리즘을 최대한 직관적으로 설명하고자 한다!
다만 베이지안 통계에 대해 어느 정도 지식이 있는 것을 전제로 글을 쓰기 때문에 이 점은 참고로 봐주시면 감사하겠습니다(?)
MC (Monte Carlo)
몬테카를로 시뮬레이션은 확률분포에서 난수를 생성하여 근사적으로 계산하는 방법이며, 사후분포를 명시적으로 정의할 수 있는 conjugate prior 관계에서는 직접 샘플링이 가능하다.
예를 들어,
- 사전분포가 베타분포(Beta distribution)를 따르고, (예. \(\theta\) ~ \(Beta(1,1)\))
- likelihood가 이항분포(Binomial distribution)를 따른다면 (예. \(Y\) ~ \(Binomial(n,k)\))
- 사후분포는 베타분포를 따르게 된다. (예. \(\theta|Y\) ~ \(Beta(1+k,1+(n-k))\))
정의된 사후분포에서 모수(\(\theta\))를 마구마구 샘플링하여 모수에 대한 분포적 특성을 추정하는 과정을 MC(Monte Carlo) 시뮬레이션이라 부른다.
이제 이런 의문이 들 수 있다. 사후분포를 명시적으로 정의할 수 있는데 왜 시뮬레이션을 하지?
사후분포가 베타분포를 따른다면 사후분포의 평균은 보지도 않고 구할 수 있다. (Beta(\(\alpha\), \(\beta\))를 따른다면, Beta 분포의 평균은 \(\frac{\alpha}{\alpha+\beta}\)가 된다.) 마찬가지로 분산도 정해진 공식에 따라 구할 수 있다. 즉, 사후분포가 정의되는 경우에는 모수의 특성을 곧바로 추정할 수 있게 되므로 시뮬레이션이 필요 없다고 느낄 수 있다.
그렇지만 \(\theta\)의 분포를 바로 정의할 수 있더라도, \(\theta^2\)의 값을 추정하는 건 차원이 다른 이야기가 되고,
만일 독립적인 두 표본의 평균 차이를 추정하고 싶다고 하면 이건 또 차원이 다른 이야기가 된다. (차원이 다르게 어려워진다는 뜻)
예를 들어 철수의 롤 실력과 영희의 롤 실력을 비교한다고 해보자. 철수의 롤 실력과 영희의 롤 실력은 각각 정규분포(normal distribution)를 따르고, 두 명의 롤 실력 기복은 일정하다고 가정(분산은 이미 상수로 정해져 있고 이를 알고 있다고 가정)해보자.
그러면 철수의 롤 실력 분포와 영희의 롤 실력 분포에서 각각 롤 실력이라는 모수를 추정할 수 있다.
하지만 P(철수의 롤 실력 - 영희의 롤 실력 > 0)이 맞는지를 추정하는 일은 grid approximation을 사용하지 않는 이상 계산이 까다롭다.
그러나 몬테카를로 시뮬레이션을 사용할 수 있으면 이를 비교적 쉽게 추정할 수 있다. 철수의 롤 실력, 영희의 롤 실력을 추출해서 값을 비교하는 것을 각각 반복하면 된다.
좀 더 자세히 이야기하면, 한 번 철수의 롤 실력, 영희의 롤 실력 표본을 추출하고 이를 비교한다. 철수의 롤 실력이 더 크다고 판단되면 1, 그렇지 않으면 0을 부여한다. 이를 10000번 반복하면서 철수의 롤 실력이 영희의 롤 실력보다 더 크게 나오는 경우를 구할 수 있게 되는데 전체 표본을 추출한 횟수에서 철수가 이겨버린 횟수를 나누면 P(철수의 롤 실력 - 영희의 롤 실력 > 0)을 추정할 수 있게 된다.

Gibbs Sampler
Gibbs sampler는 사후분포가 명시적으로 conjugate하지는 않지만 full conditional posterior distribution은 conjugate 한 경우, 대충 말하면(?) 사후분포가 conjugate하지는 않지만 조건부로 conjugate한 경우에 사용할 수 있는 알고리즘이다.
정규분포로 예를 들어보자. 위에서는 분산이 알려져 있다고 가정했지만 실전에서는 분산이 알려져 있을 리가 없다. 즉, 원래는 분산 역시도 우리가 추정해야 하는 모수이다.
분산의 사전분포는 일반적으로 inverse-gamma distribution (감마분포의 역함수)를 따른다고 가정한다. (다른 말로 하면 1/분산이 gamma distribution을 따른다고도 할 수 있다.)
분산의 사후분포는 특정 조건을 따르지 않으면 inverse-gamma 분포를 따른다고 정의할 수 없지만, 만일 평균을 조건부로 둔다면 inverse-gamma 분포를 따른다고 할 수 있다.
- 사전분포가 다음과 같을 때, \(\sigma\) ~inverse-gamma(\(\alpha, \beta\))
- \(\sigma | Y_1, Y_2, ...., Y_n\) 는 inverse-gamma 분포를 따르지 않을 수도 있지만,
- 평균을 조건부로 둔다면 즉, \(\sigma | \mu, Y_1, Y_2, ...., Y_n\) 는 inverse-gamma(\(\alpha + n/2, \beta + \frac{(X_i - \bar{X})^2}{2}\)) 을 따르게 되면서 조건부로 사후분포를 정의할 수 있게 된다.
뜬금없이 느껴질 수 있지만, 여기에 수식을 쓰면 일이 복잡해지기 때문에 증명과정은 유튜브 링크로 대체해 본다.

사후분포에 평균을 조건부로 둔다는 것은 어쨌든 평균을 알고 있어야 한다는 이야기다. 그러나 일반적으로 정규분포에서 평균은 추정해야 하는 모수이기 때문에 평균에 대한 사후분포 역시 구해야 한다. 평균에 대한 사후분포는 분산을 알고 있다는 가정 하에서 구하기 때문에 이건 자연스럽게 분산을 조건부로 둔 형태로 구해지게 된다. 즉, 평균에 대한 사후분포는 분산을 조건부로 둔 full conditional한 사후분포와 동일하며, 이 경우는 자연스럽게 사후분포가 normal distribution로서 conjugate한 분포가 나오게 된다.
복잡하게 설명하긴 했지만,
- 평균의 사후분포는 분산과 데이터를 알고 있다는 전제 하에서 정규분포를 따르고,
- 분산의 사후분포는 만일 평균을 알고 있다는 전제라면 inverse-gamma 분포를 따른다고 정의할 수 있게 된다.
그러면 분산을 직관 또는 참고 데이터에 기반하여 정의한 다음, 평균의 사후분포인 정규분포에 분산을 대입해서 평균을 랜덤하게 하나 뽑을 수 있다. 거기서 랜덤하게 뽑은 평균을 다시 분산의 조건부 사후분포에 대입해서 분산을 다시 하나 랜덤하게 뽑을 수 있다.
\(\sigma_1\)을 먼저 대입해서 \(\mu_1\)를 얻고, 이걸 대입해서 \(\sigma_2\)를 얻고, 이걸 다시 대입해서 \(\mu_2\)를 얻고... 이런 식으로 반복해나가다보면 우리가 알고자 하는 모수에 대한 정보를 시뮬레이션할 수 있는데 이러한 과정을 Gibbs Sampler 알고리즘이라고 부른다.
이를 좀 더 있어 보이게 수식으로 표현하면,
1. \(\theta\)를 추출한다. : \( \theta^{(s+1)} \sim p(\theta \mid \tilde{\sigma}^{2 (s)}, y_1, \dots, y_n) \)
2. \(\sigma\)를 추출한다. : \( \tilde{\sigma}^{2 (s+1)} \sim p(\tilde{\sigma}^2 \mid \theta^{(s+1)}, y_1, \dots, y_n) \)
3. \(\theta\)와 \(\sigma\)를 하나의 순서쌍으로 만들어 놓는다.(parameter의 집합이라고 보면 된다.): \( \phi^{(s+1)} = \{ \theta^{(s+1)}, \tilde{\sigma}^{2 (s+1)} \} \)
이렇게 되면, s번째 모수의 순서쌍은 s-1번째 모수의 순서쌍에만 영향을 받게 된다. 1번째 ~ s-2번째의 순서쌍이 이미 존재해도 결국 대입하는 건 이전의 모수에 대한 정보이기 때문에 이를 Markov Chain 과정이라고 부른다. Markov Chain은 현재 상태가 주어졌을 때, 미래 상태가 오직 현재 상태에만 의존하는 확률 과정을 의미한다.
Gibbs Sampler는 Markov Chain 과정에 의해(이전 모수에만 의존함) 확률분포에서 난수를 생성하므로 Markov Chain Monte Carlo(MCMC)의 일종인 알고리즘이라 볼 수 있다.
Gibbs Sampler의 특징
Gibbs Sampler는 이전 값에 영향을 받기 때문에 현재의 값은 이전의 값과 상관관계를 가질 수 있다. 이를 auto-correlation(자기 상관)이라고 부르는데, 만일 auto-correlation이 크다면 현재의 값은 이전의 값과 비슷한 값만 계속 뭉텅이로 뽑히게 된다.
모수의 분포를 파악하기 위해서는 최대한 넓은 범위를 탐색하는 것이 중요한데 자칫 잘못해서 비슷한 값만 추출하게 된다면 우리는 충분한 표본을 뽑기 전까지 비슷한 범위에서 뽑힌 모수만 보고 잘못된 결론을 내리게 될 수도 있다. 이를 stuck 된다고 표현한다.(적절한 한국어 용어는 모르겠다..) 이를 방지하려면 Burn-in을 설정하거나 샘플링 간격을 넓히는(Thinning) 방법이 있다.
MC 알고리즘은 사후분포에서 표본을 독립적으로 뽑는 것을 가정하기 때문에 auto-correlation이 없지만, MCMC 알고리즘인 Gibbs Sampler는 상관관계가 있는 상태에서 뽑기 때문에 일반적으로 MC 알고리즘에 비해 정보가 부족하다. 가령 MC 알고리즘만으로는 1,000여 개의 표본만 있어도 되는데 MCMC 알고리즘은 비슷한 값을 탐색하는 것을 감안해서 10,000여 개의 표본을 추출해야 할 수도 있다.
만일 MC 알고리즘에서 추출한 1,000여개의 표본과 MCMC 알고리즘에서 추출한 10,000여개의 표본이 비슷한 수준의 정보를 갖는다면 MCMC 알고리즘은 MC 알고리즘보다 10배의 표본을 더 뽑아야 하는데, 이때의 10이라는 숫자는 effective size로 볼 수 있다.
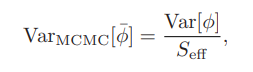
엄밀하게 effective size는 위의 이미지처럼 MCMC 알고리즘을 통해 얻은 모수의 분산과, MC 알고리즘을 통해 얻은 모수의 분산이 어느 정도 차이 나는지를 비교하여 구한다.
Metropolis 알고리즘
Gibbs Sampler는 부분적으로 conjugate한 경우엔 좋지만, 아예 conjugate 관계가 없는 경우엔 어떻게 해야 할까? 여기서 등장하는 게 Metropolis 알고리즘이다.
사후분포를 명확하게 정의할 수 없는 경우에 대해 생각해 보자. MC 알고리즘은 사후분포가 사전분포와 conjugate 한 관계를 가진다면 바로 사용할 수 있고, Gibbs Sampler는 사후분포가 조건부로 사전분포와 conjugate한 관계를 가진다면 바로 사용할 수 있다.
그러나 conjugate하지 않아서 사후분포를 명확하게 정의할 수 없는 경우에는 위 두 개 방법을 사용할 수 없기 때문에 다른 방법을 강구해야 한다.
일종의 모수(parameter) 보따리가 있다고 가정해 보자. 이 보따리를 통해 얻을 수 있는 결과보다 더 좋은 결과를 얻을 수 있는 보따리가 있다면 다른 보따리에서 모수를 좀 더 추가해야 할 것이다. 일반적으로 우리는 A가 B보다 좋다는 것을 확인하기 위해 비율을 통해 확인하곤 하는데,
\(\frac{\#\{\theta^{(s)} \text{ in the collection } = \theta_a\}}{\#\{\theta^{(s)} \text{ in the collection } = \theta_b\}} \approx \frac{p(\theta_a \mid y)}{p(\theta_b \mid y)} \)
이를 수식으로 표현하면 다음과 같다.
만일 기준 모수인 \(\theta_b\)보다 \(\theta_a\)가 더 좋다면 우리는 겸허히 \(\theta_b\)의 모수 보따리(집합)를 받아들여야 할 것이다. 만일 \(\theta_b\)가 \(\theta_a\)보다 결과가 좋지 않더라도 \(\theta_b\)를 무조건 버리지는 않는다. 한 번 더 랜덤 가챠(?)를 돌려서 이 확률을 뚫어낸다면 \(\theta_b\)를 수용하게 된다.
즉, uniform(0, 1)에서 랜덤으로 뽑은 확률(=u)과 \(\theta_b\)와 \(\theta_a\)의 비율(=r)을 비교해서, 만일 r이 랜덤 확률 u보다 크다면 새로운 \(\theta_b\)를 선택한다.
좀 더 엄밀하게 정의해서 쓰면,
새로운 모수의 사후분포와 기존 모수의 사후분포의 비율인 r =\(\frac{P(\theta^*|Y)}{P(\theta_{(s)}|Y)}\) 을 구하고,
- 만일 r이 1보다 크거나 같다면 새로운 모수를 받아들이고,
- r이 1보다 작다면 랜덤으로 확률을 추출해서 r과 비교한 후 새로운 모수를 받아들일지 말지를 결정한다.
새로운 \(\theta\)는 제안 분포(proposal distribution)에서 랜덤으로 추출하는데, 만일 이 제안 분포가 정규분포, 균일분포와 같이 대칭적인 형태를 띤다면 위 수식대로 그냥 r을 구해서 사용하면 된다. 만일 제안분포가 비대칭이라면 이를 Metropolis-Hastings 알고리즘이라고 부른다. 제안분포가 비대칭이면, 샘플을 제안할 확률 자체가 다르기 때문에 이를 보정하는 추가 과정이 필요하지만, 이 글에서는 추가 과정에 대한 내용은 생략한다.
요악하면, MC, Gibbs Sampler, Metropolis 알고리즘은 베이지안 통계에서 확률을 복잡하게 계산하지 않고 시뮬레이션을 통해 이를 해결하도록 만들어준다. 다만, 상황에 따라 사용할 수 있는 알고리즘이 다르기 때문에 적절한 알고리즘을 잘 선택하는 것이 중요하다 할 수 있겠다.
참고자료
- A First Course in Bayesian Statistical Methods
'Statistics' 카테고리의 다른 글
| 로지스틱 회귀분석, 짤막하게 개념 훑기 (1) | 2025.05.24 |
|---|---|
| 인과추론, 입문을 원하신다면 이런 책은 어떠신가요? (0) | 2025.02.15 |
| 베이지안 통계 - 기본 개념 가볍게 살펴보기 (0) | 2025.01.12 |
| 가상의 게임 데이터로 살펴보는 이중차분법 (feat. 🧙♂️법사야캐요) (0) | 2024.12.30 |
| 인과추론 학습기 - 개입과 뒷문 기준 (2) | 2024.11.01 |
